The vertices of a triangle are (2,4),B(2,6),C(2+√3,5). The triangle is :Solution in Tamil
Step by step video & image solution for The vertices of a triangle are (2, 4), B (2,6),C (2+ sqrt3,5). The triangle is : by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CO-ORDINATE GEOMETRY BOOK - CHETAN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - ASSIGNMENT-5
11 Videos
- CO-ORDINATE GEOMETRY BOOK - CHETAN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - PROBLEM SET - 5.1
4 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):
3 Videos
- FINANCIAL PLANNINGBOOK - CHETAN PUBLICATIONCHAPTER - FINANCIAL PLANNINGEXERCISE - ASSIGNMENT-4
16 Videos
Similar Questions
Slope of a line is √3. Find its inclination.
View SolutionShow that A(4,−1),B(6,0),C(7,−2)andD(5,−3) are vertices of a square.
View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.
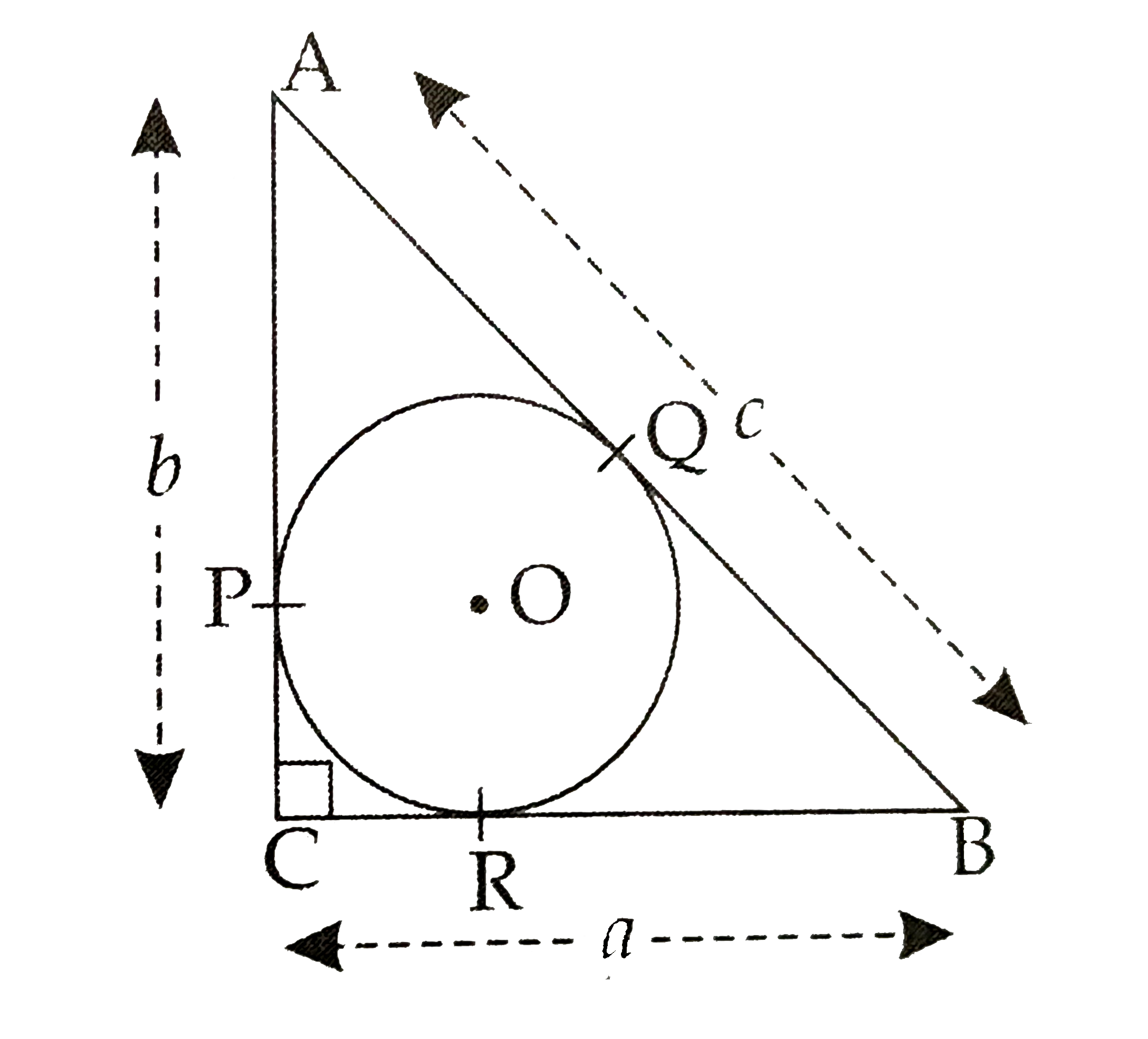
View SolutionChoose correct alternative for each of the following questions:
(1) Rate of GST on essential commodities is ……..
View SolutionThe vertices of a triangle are (2,4),B(2,6),C(2+sqrt(3),5). The triangle is
View SolutionThe area of triangle formed by vertices are (b,c),(c,a) and (a,b) is Delta, and the area of triangle whose vertices are (ac-b^(2),ab-c^(2)),(ab-c^(2),bc-a^(2)) and (bc-a^(2),ac-b^(2)) is Delta'. If a,b,c represent the sides of triangle of perimeter 16. Then the value of (Delta')/(64Delta)=
View SolutionThe vertices of a triangle are A(−2,1),B(6,−2)andC(4,3). Find the equation of the altitudes of the triangle.
View SolutionIf A(3, 5, -4), B(-1, 1, 2) and C(-5, -5, -2) are the vertices of Δ ABC, then the triangle is
View SolutionThe triangle with vertices (2,4), (2,6) and (2+√3 ,5) is
View SolutionDeterime whether the points are vertices of a right triangle A(-3,-4),B(2,6) and C(-6,10).
View SolutionThe triangle with vertices A (2,4), B (2,6) and C (2+√3, 5) is
View SolutionShow that the points
(2,4),(2,6)(2+√3,5) form an equilateral triangle.
View SolutionA (4,8), B(-2,6) are two vertices of a triangle ABC. Find the coordinates of C if the centroid of the triangle is (2,7).
View SolutionShow that the points (2,4),(2,6) and (2+√3,5) are the vertices of an equilateral triangle.
View SolutionA(-1, 3), B(4, 2) and C(3, -2) are the vertices of a triangle.
Find the coordinates of the centroid G of the triangle.
View SolutionA (1, -5), B (2, 2) and C (-2, 4) are the vertices of triangle ABC. find the equation of:
the median of the triangle through A.
View Solution
