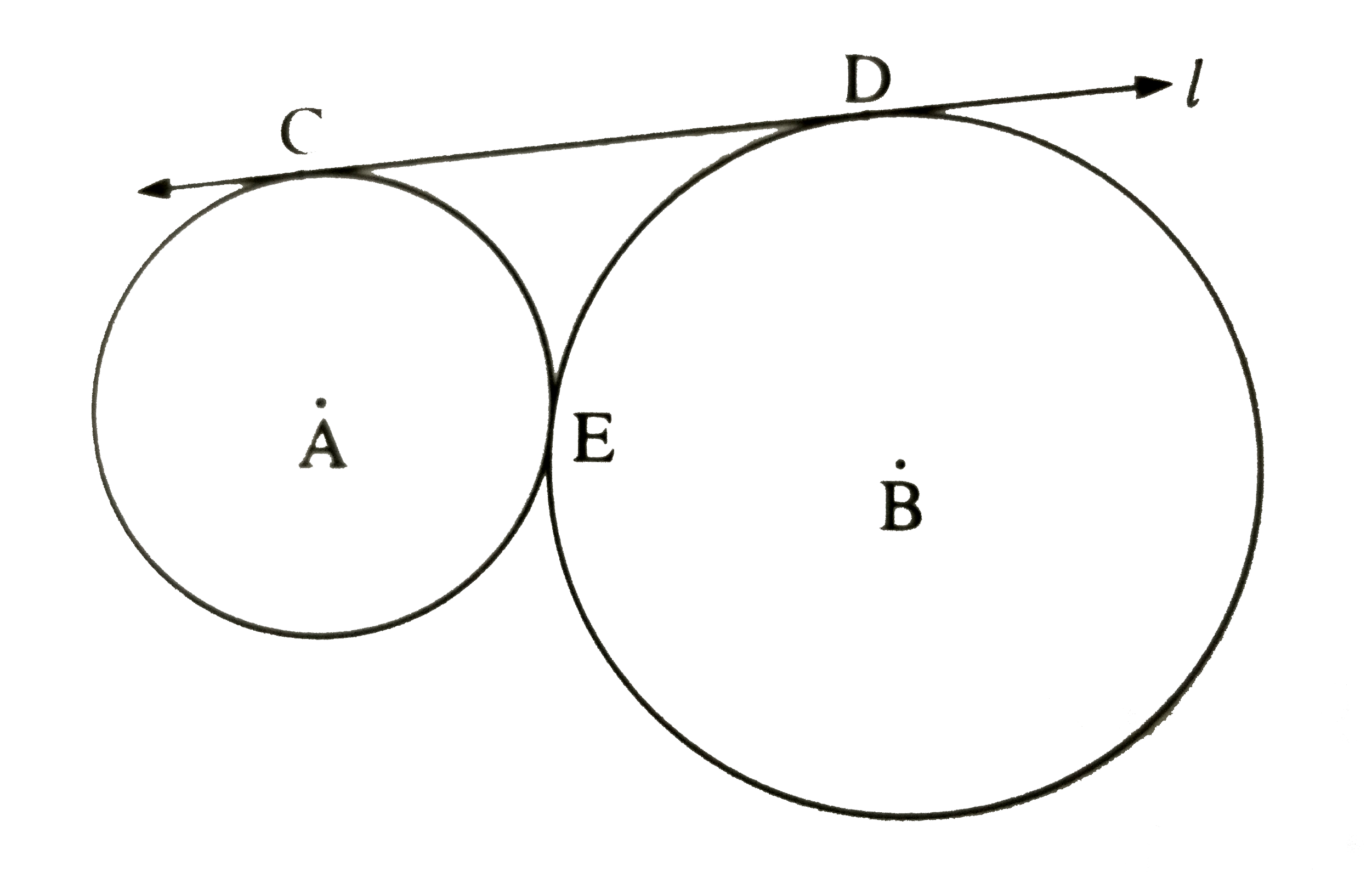
In the adjoining figure, the circles with centres A and B touch each other at E Line l is a common tangent that touches the circles at C and D respectively. Find length of seg CD if the radii of the circles are 4 cm, 6 cm ?
Construction :
Draw seg AE and seg EB.
Draw seg AF ⊥ seg BD, B - F- D
 Solution in Tamil
Solution in Tamil
Step by step video & image solution for In the adjoining figure, the circles with centres A and B touch each other at E Line l is a common tangent that touches the circles at C and D respectively. Find length of seg CD if the radii of the circles are 4 cm, 6 cm ? Construction : Draw seg AE and seg EB. Draw seg AF bot seg BD, B - F- D by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set - 3.3
3 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Practice Set - 3.4
7 Videos
- CIRCLEBOOK - CHETAN PUBLICATIONCHAPTER - CIRCLEEXERCISE - Assignment - 3 (Solve any two of the following questions):
3 Videos
- CHALLENGING QUESTIONSBOOK - CHETAN PUBLICATIONCHAPTER - CHALLENGING QUESTIONSEXERCISE - Mensuration
9 Videos
- CO-ORDINATE GEOMETRY BOOK - CHETAN PUBLICATIONCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - ASSIGNMENT-5
11 Videos
Similar Questions
In the adjoining figure, G, D, E, F are concyclic points of a circle with centre C . ∠ECF=70∘ m (arc DGF) =200∘ find
(i) m arc DE
(iii) m (arc DEF).

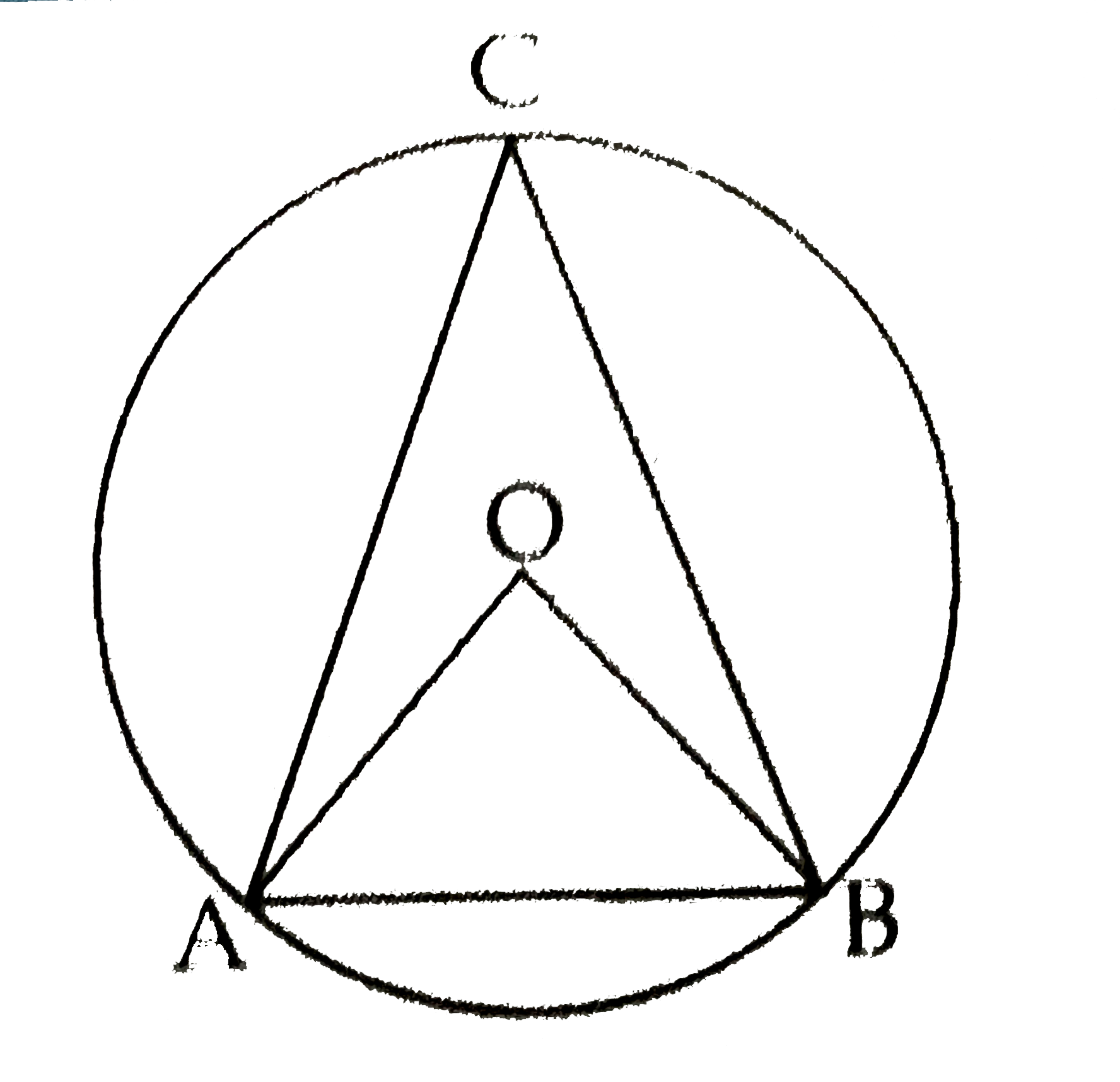
View SolutionIn the abjoining figure, point O is the centre of the circle . Length of chord AB is equal to the radius of the circle . Find
(i) ∠AOB
(ii) ∠ACB
(iii) nm (arc AB)
(iv) m (arc ACB)
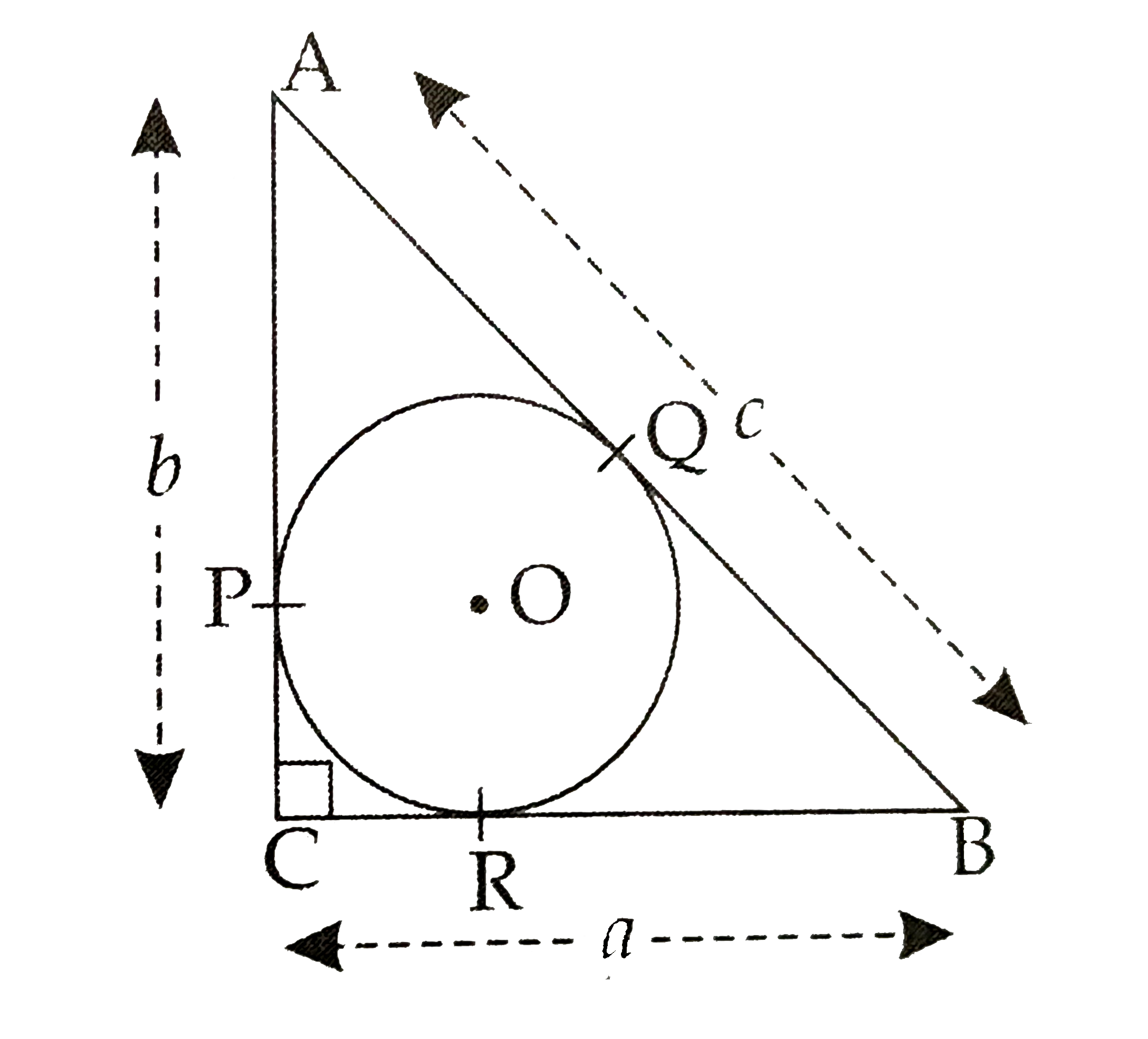
View SolutionA circle with centre 'O' is incircle of ΔABC.ΔBCA=90∘ . Radius of the circle is r.
Prove that : 2r = a + b - c.
View SolutionA tin maker converts a cubical metalic box into 10 cylindrical tins. Side of the cube is 50 cm and radius of the cylindrical is 7cm. Find the height of each cylinder so made if the wastage incurred was 12%. (π=227)
View SolutionSlope of a line is √3. Find its inclination.
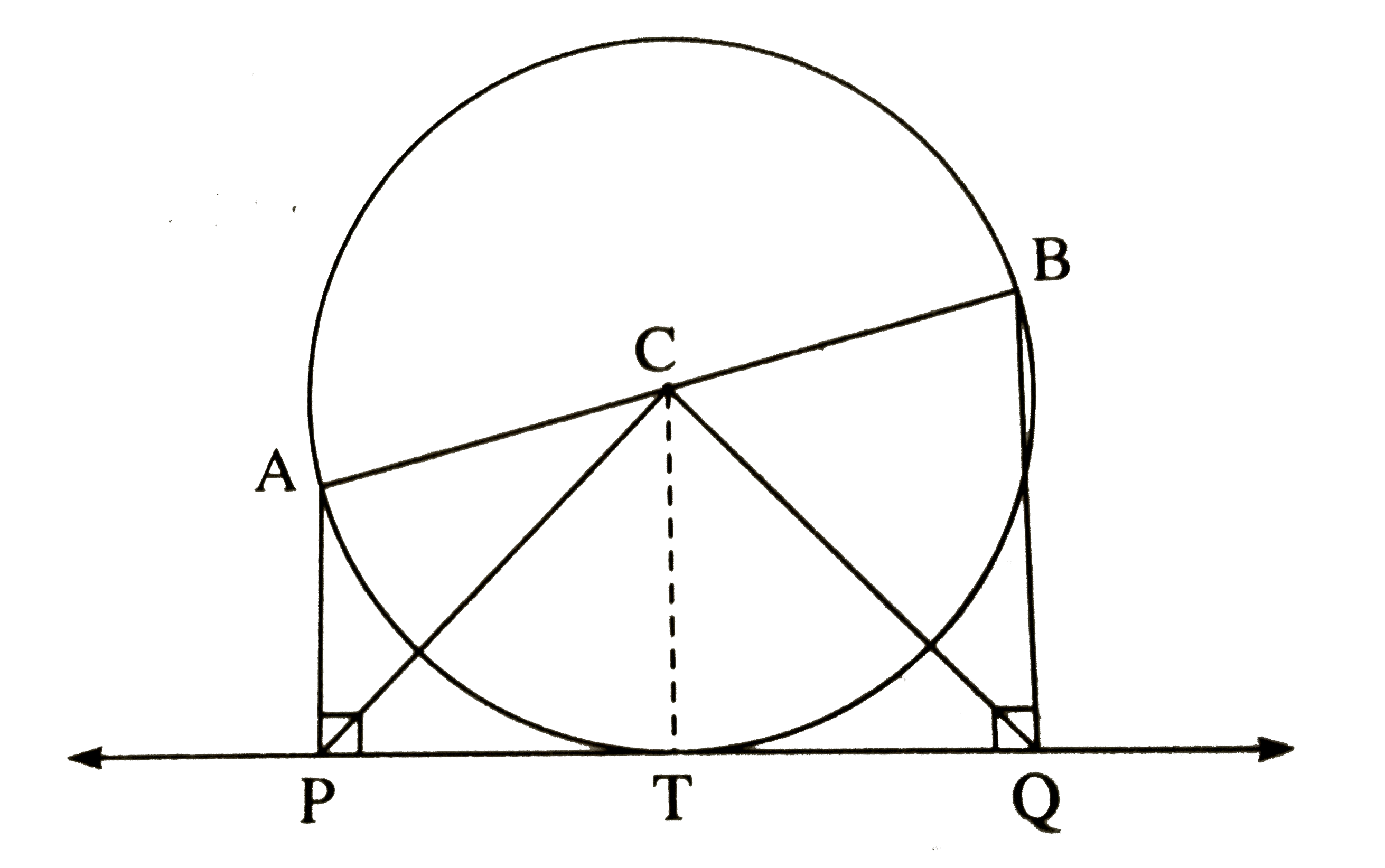
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

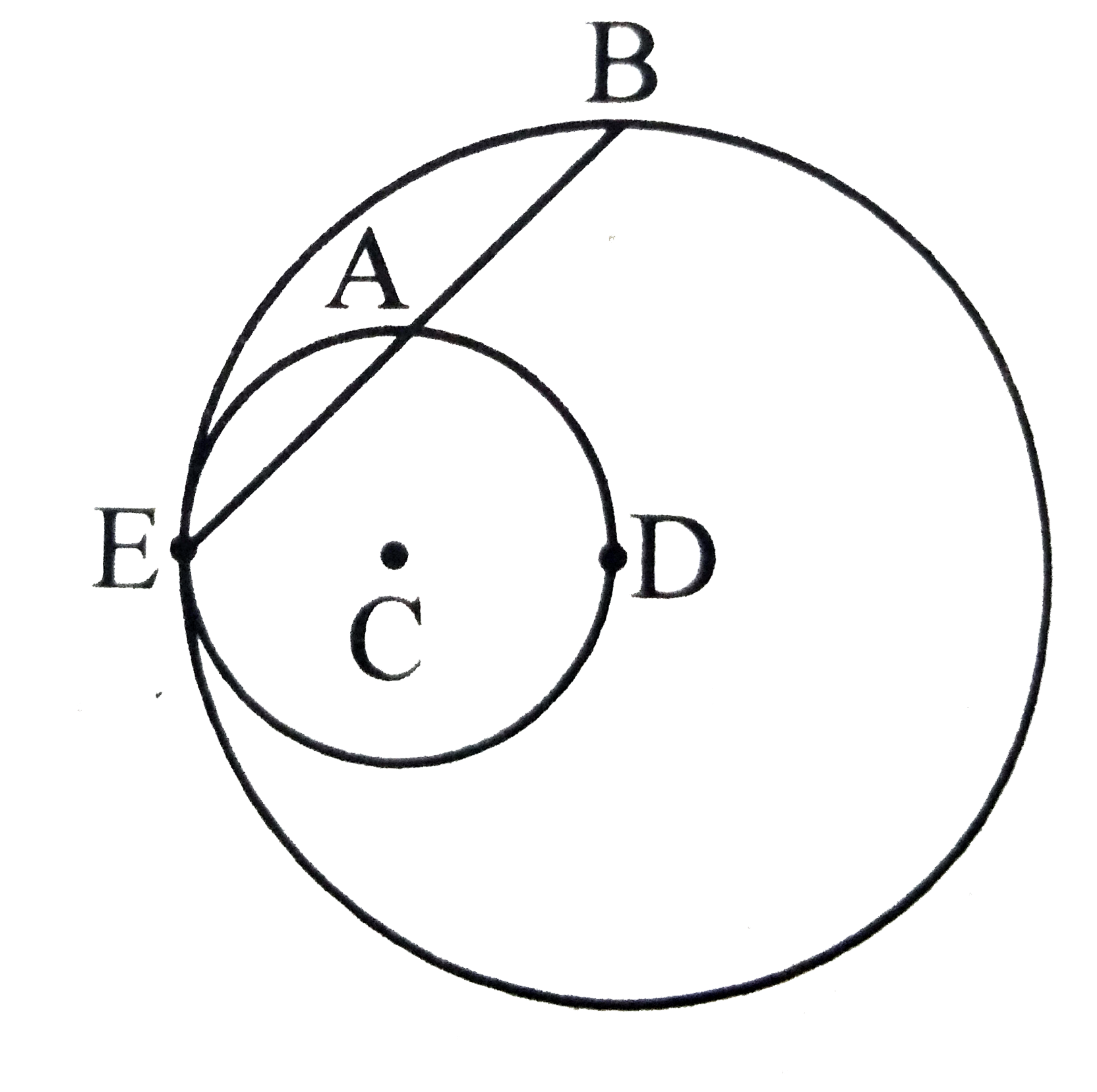
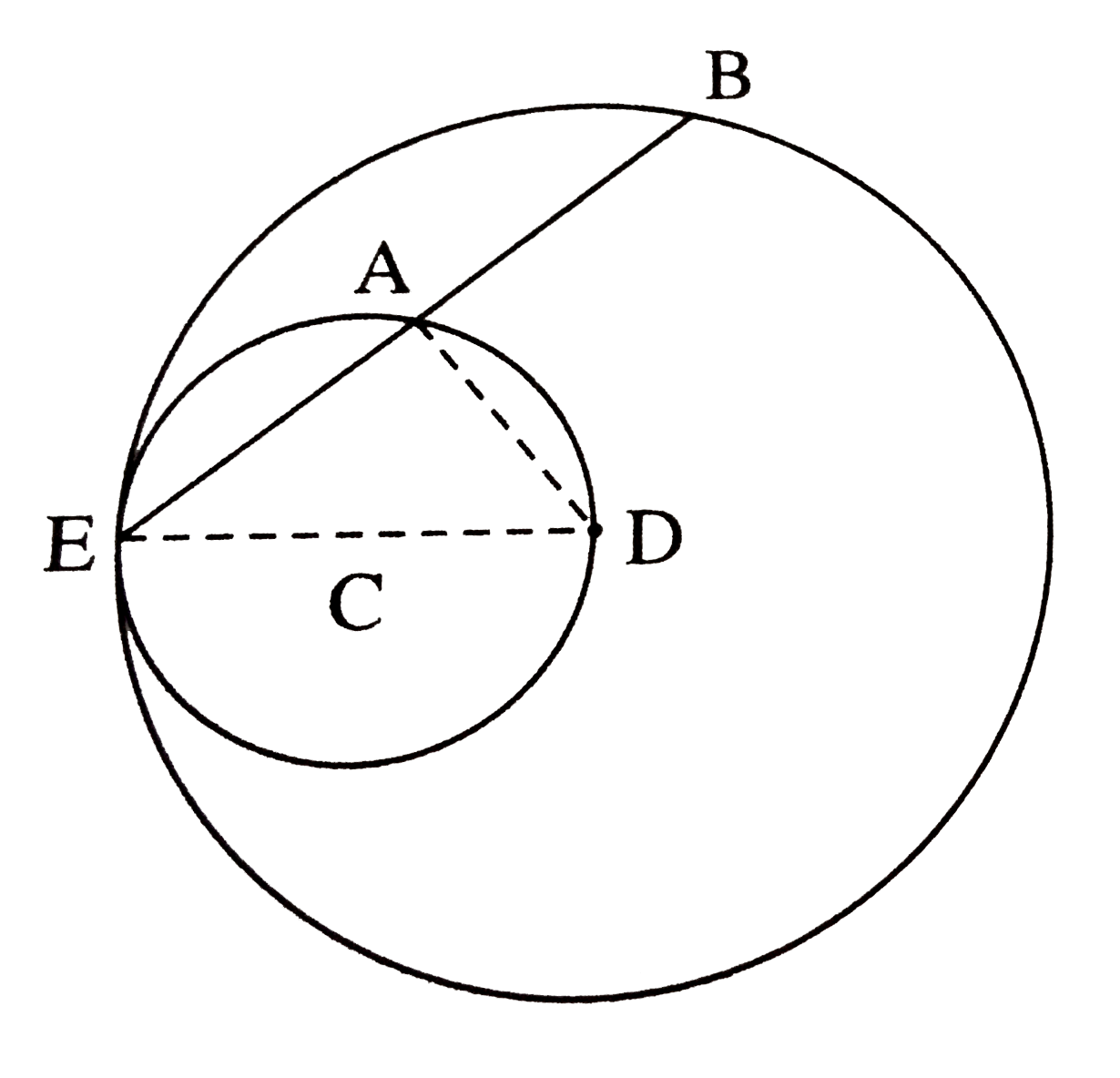
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
View SolutionAs shown in the adjoining figure , two circles centred at A and B are touching at C. Line passing through C intersects the two circles at M and N respectively.
Show that seg AM ∣∣seg BN.
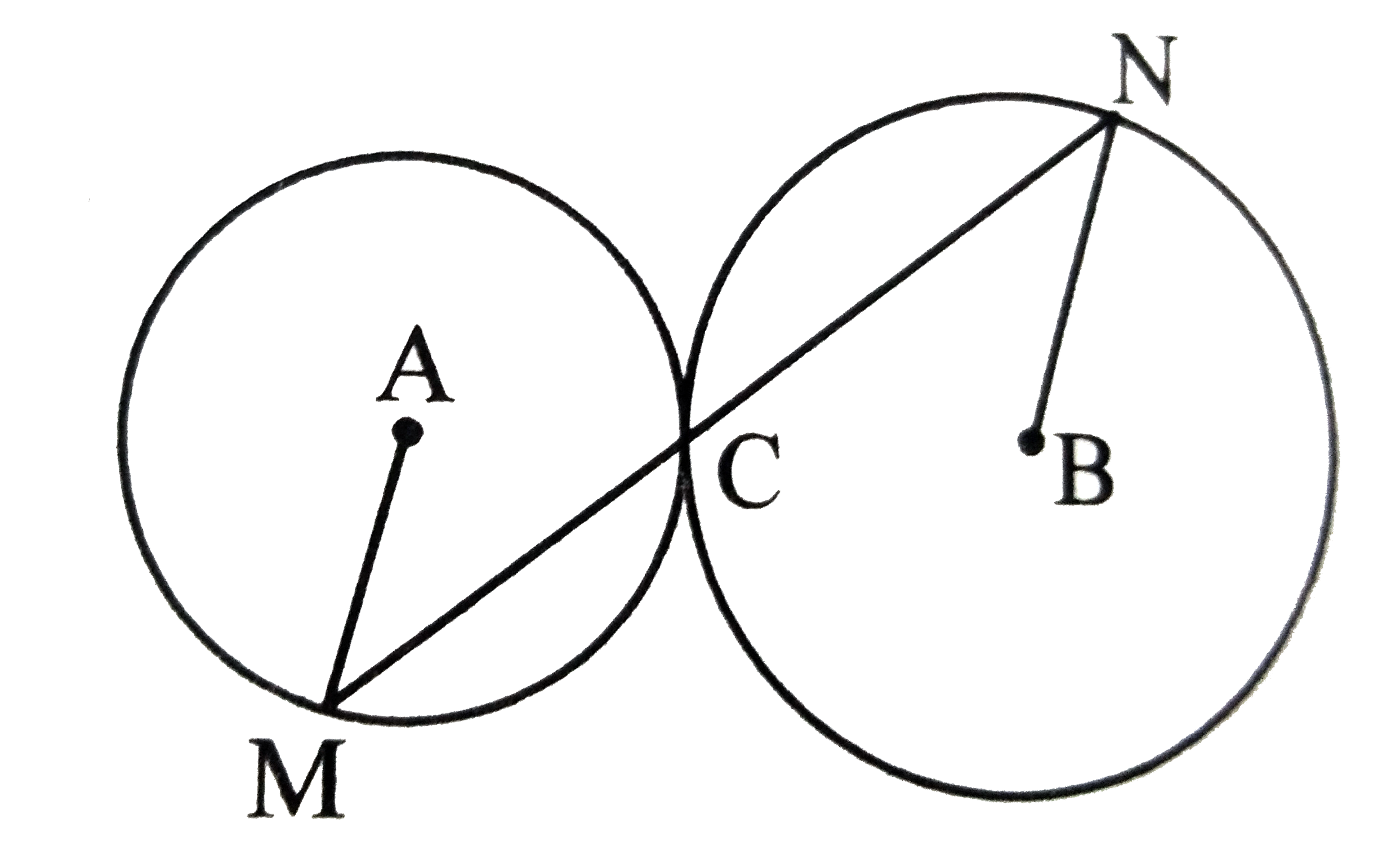
View SolutionIn the figure, the circles with centeres A and B touch each other at E. Line l is a common tangent which touches the circles at C and D respectively. Find the length of seg CD, if the radii of the circle are 4 cm, 6 cm.
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
View SolutionIn figure, circles with centers C and D touch internally at point E. D lies on the inner circle. Chrd EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.
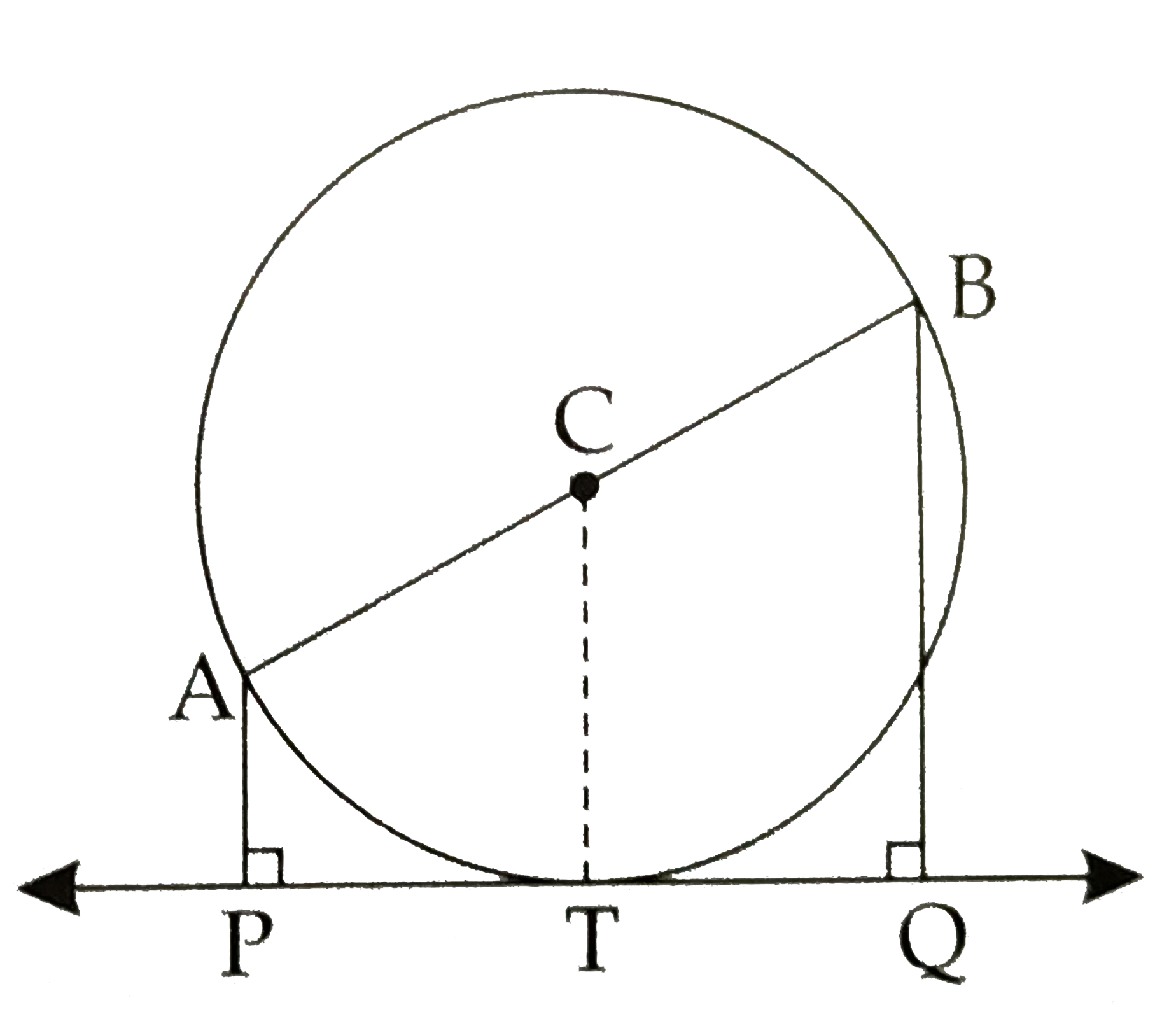
View SolutionIn the adjoining figure, seg AB is a diameter of a circle with centre C . Line PQ is a tangent, it touhces the circle at T. segs AP and BQ are perpendiculars to line PQ. Prove seg CP ≅ seg CQ .
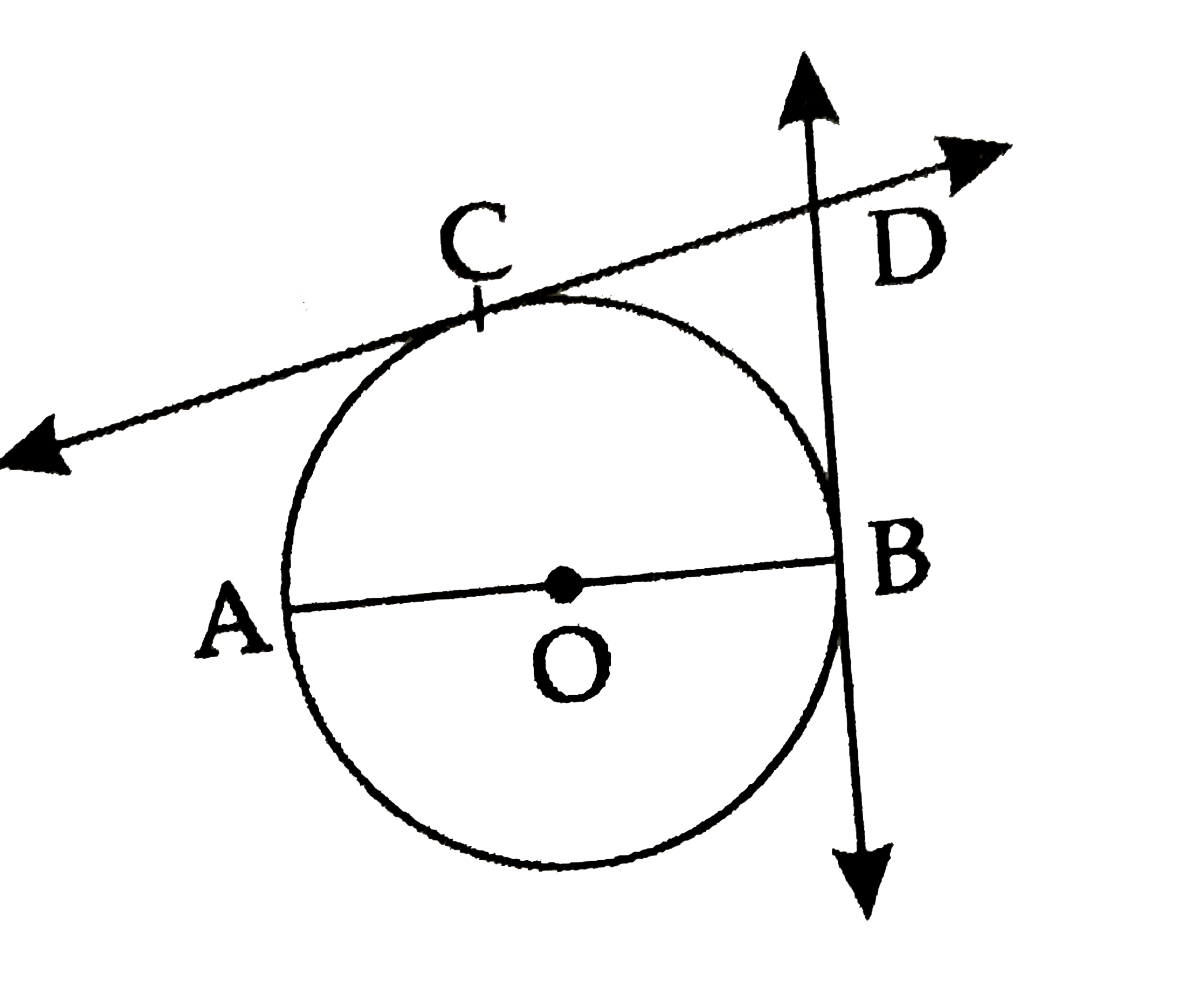
View SolutionIn the adjoining figure, O is the centre and seg AB is a diameter. At point C on the circle, the tangent CD is drawn. Line BD is tangent at B . Prove that seg OD ∣∣ seg AC.
View SolutionAs shown in the adjioning figure, two circles interset each other in points A and B. Two tangents touch these in point these circles in points P,Q and R, S as shown . Line AB intersects seg PQ in C and seg RS in D. Show that Cand D are midpoints of seg PQ and seg RS respectively.
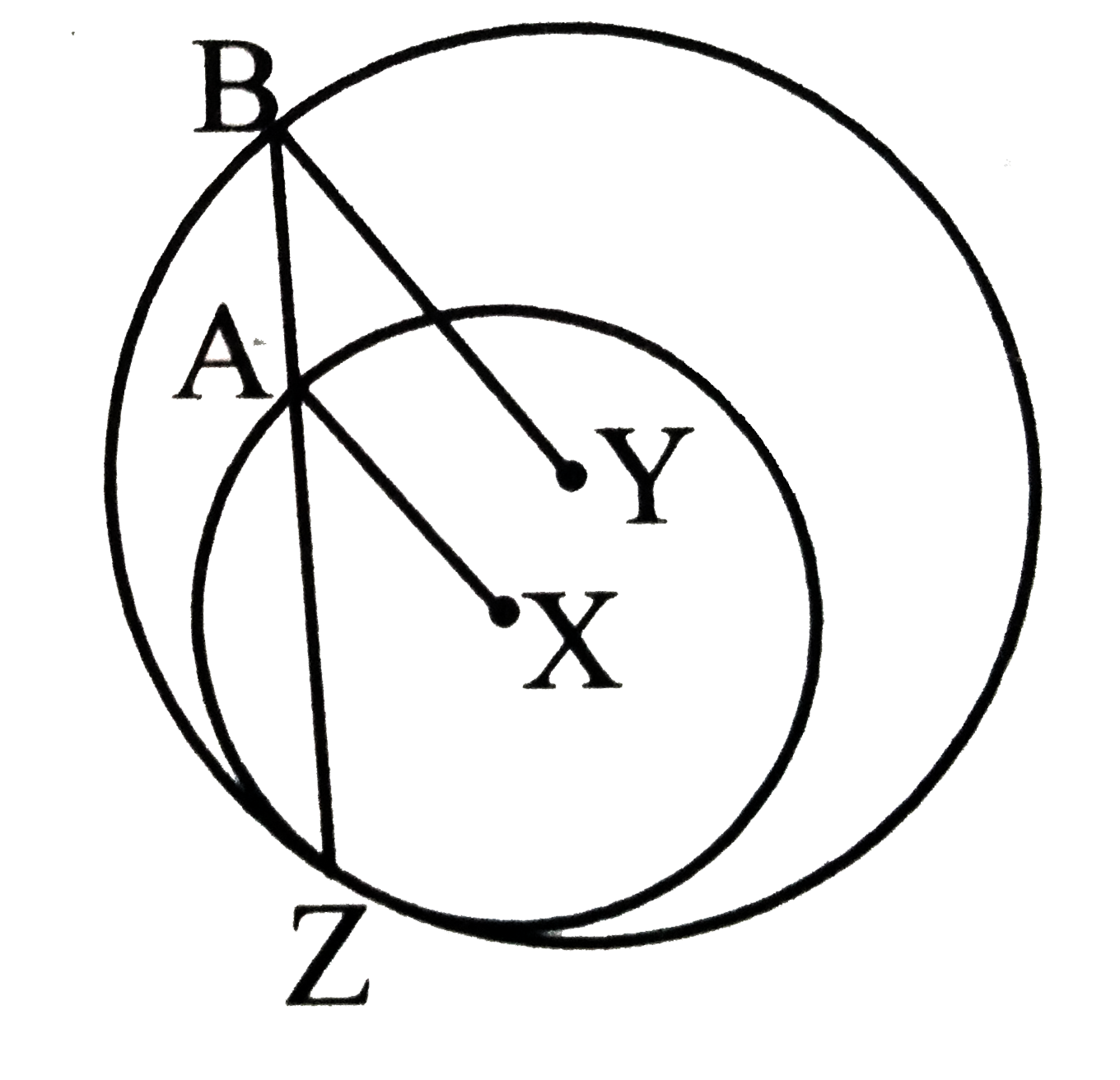
View SolutionIn the adjoining figure, circles with centres X and Y touch internally
at point Z. Seg BZ is a chord of bigger circle and it intersects smallest
circle at point A. prove that, seg AX ∣∣seg BY.
View Solution
