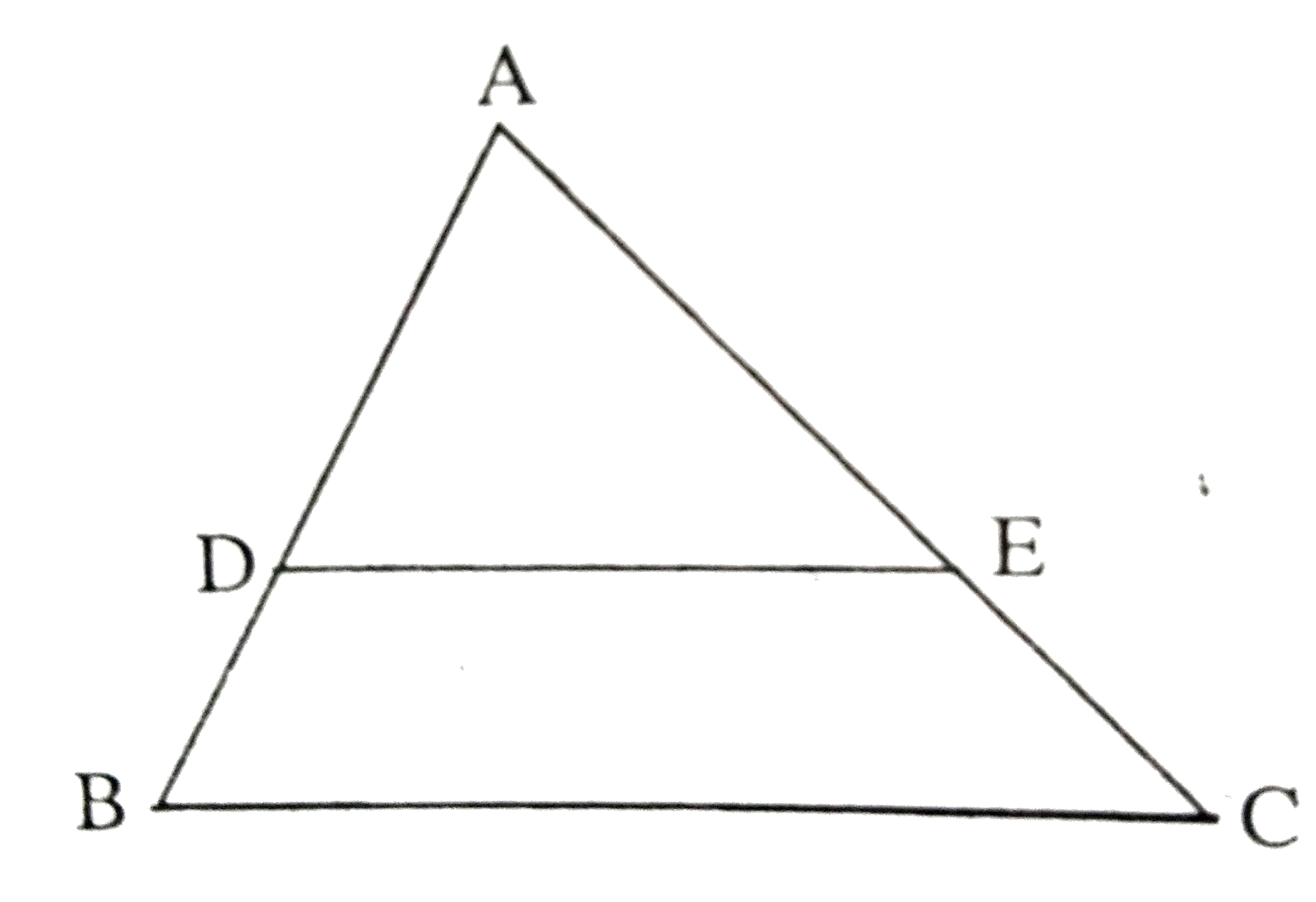
The point D and E are situated on the sides AB and AC of ΔABC in such a way that DE∣∣BC and AD:DB=3:1, If EA=3.3cm, then the length of AC isSolution in Bengali
1.1cm
4cm
4.4cm
5.5cm
∵ in ΔABC, DE∣∣BC,
∴ by Thales' theorem we get, ADBD=AECE or, BDAD=CEAE
or, BD+ADAD=CE+AEAE
or, 43=AC3.3 [∵AD:DB=3:1 or, BDAD=13 or, 3AC=4×3.3 or, AD+BDAD=3+13=43]
or, AC=4×3.33 or, AC=4.4
∴AC=4.4cm, ∴(c) is correct.
Topper's Solved these Questions
- SIMILARITYBook:CALCUTTA BOOK HOUSEChapter:SIMILARITYExercise:Exercise 5.1
Explore 32 Videos
- SIMILARITYBook:CALCUTTA BOOK HOUSEChapter:SIMILARITYExercise:Exercise 5.2
Explore 27 Videos
- SAMPLE QUESTIONS PAPERSBook:CALCUTTA BOOK HOUSEChapter:SAMPLE QUESTIONS PAPERSExercise:QUESTION
Explore 157 Videos
- SIMPLE INTERESTBook:CALCUTTA BOOK HOUSEChapter:SIMPLE INTERESTExercise:Long-answer type questions
Explore 37 Videos
Similar Questions
In the following figure , ∠P=
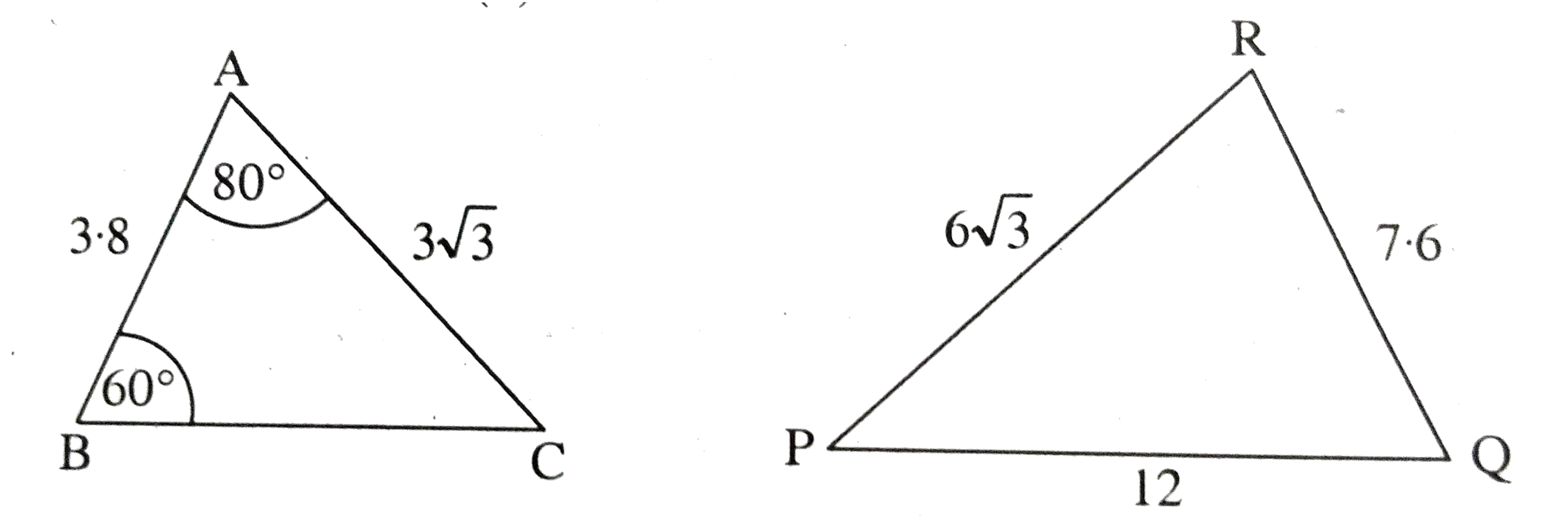
View SolutionIn ΔPQR and ΔDEF, PQDE=QREF=RPFD. Then which one of the following is correct?
View SolutionA person deposite ₹ 100 in a bank and after 2 yars he got a total ₹121 as a return. Then the componund interest of the bank per annum is
View SolutionGoutam took a loan of some money from a cooperative bank for opening a poultry farm at the rate of simple interest of 12% per annum. Every month he has to repay 378Rs as interest. Determine the loan amount taken by him.
View SolutionIn ABC, DE is parallel to base BC , with D on AB and E on AC . If ADDB=23 , find BCDE .
View SolutionΔABC में बिंदु D तथा E भुजा AB तथा AC पर इस प्रकार है की AD = 13AB , AE = 13 AC है, यदि BC की लम्बाई 15 cm हो, तो DE की लम्बाई 15 cm हो, तो DE की लम्बाई ज्ञात करे?
View SolutionΔABC में, बिंदु D तथा E, भुजा AB तथा AC पर इस प्रकार है की DE∣∣BC तथा DE, ΔABC के क्षेत्रफल को दो बराबर भागो में बाटता है। AD तथा BD का अनुपात ज्ञात करे?
View SolutionΔABC में, DE∣∣AC, D तथा E, भुजा AB तथा BC पर दो बिंदु हे| यदि AB=10cm तथा AD=4cm हे, तब BE:CE हे|
View SolutionΔABC में भुजाओ AB और AC पर क्रमश: बिंदु D और E इस प्रकार है कि DE∣∣BC तथा AD:DB=3:1 है | यदि EA=3.3 सेमी., तो AC =
View SolutionIn △ABC, D and E are points on the sides AB and AC respectively such that DE∣∣BC. If ADDB=34andAC=15cm find AE.
View SolutionIn the given Fig. 3, in ΔABC,DandE are the mid point of the sides AB and AC respectively. Find the length of DE. Prove that DE=12BC.
View SolutionIn ΔABC, D and E are points on AB and AC respectively, such that DE∣∣BC. If ADDB=413 and AC = 20.4 cm, find AE.
View SolutionIn ΔABC,D and E are points on side AB and AC respectively such that DE∣∣BC and AD:DB=3, If EA=3.3cm, them find AC.
View SolutionΔABC में बिन्दु D और E क्रमश : भुजाओं AB और AC पर इस प्रकार है कि DE∣∣BC.
यदि ADDB=12और AC=27cm तो EC=
View SolutionIn a ΔABC,AB=AC,D is a point on BC such that ∠BAD=50∘ and a point E on side AC such that AE = AD find ∠CDE.
View Solution

