If S,S′ are the foci and P any point on the hyperbola x2−y2=a2, prove that, ¯¯¯¯¯SP.¯¯¯¯¯¯¯S'P=CP2, where C is the centre of the hyperbola. Solution in Bengali
Step by step video & image solution for If S,S^(') are the foci and P any point on the hyperbola x^(2) - y^(2) = a^(2), prove that, bar(SP).bar(S^('P)) = CP^(2), where C is the centre of the hyperbola. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - MULTIPLE CHOICE TYPE QUESTIONS20videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHOT ANSWER TYPE QUESTIONS16videos
HYPERBOLA
- BOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)7videos
DIAGRAMMATIC REPRESENTATION OF DATA
- BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams20videos
MATHEMATICAL INDUCTION
Similar Questions
If e is the eccentricity of the hyperbola x2a2−y2b2=1 , then e =
06:23View SolutionExplain what geometrical diagrams are represented by the equatio x2a2+y2a2(1−e2)=1, where a and e are constants.
View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
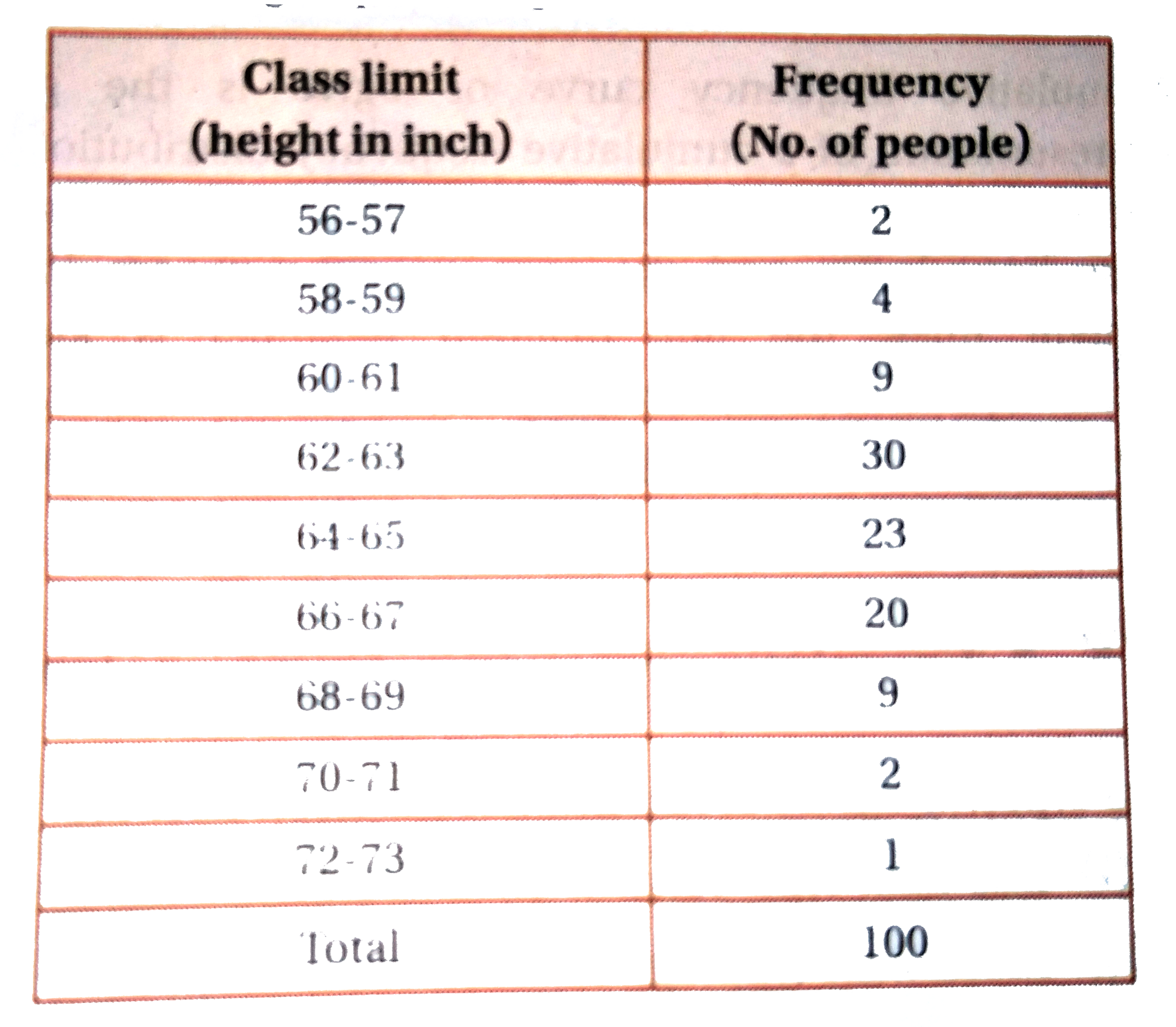Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches. 04:16View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
View SolutionIf S ans S' are the foci,C is the center,and P is point on the rectangular hyperbola,show that SP xx SP=(CP)^(2)
08:12View SolutionIn a rectangular hyperbola x2−y2=a , prove that SP⋅S'P=CP2 where P is any point on the hyperbola, C is origin and S and S' are foci.
11:08View Solutionकिसी समकोणीय अतिपरवलय x2−y2=a2 में सिद्ध कीजिए कि SP.S'P=CP2 जहाँ अतिपरवलय पर कोई बिन्दु C मूल बिन्दु, S तथा S' अतिपरवलय कि नाभियाँ है |
08:37View Solutionकिसी समकोणीय अतिपरवलय x2−y2=a2 में सिद्ध कीजिए कि SP×S'P=CP2 जहाँ P अतिपरवलय पर कोई बिंदु , C मूलबिन्दु, S तथा S' अतिपरवलय कि नाभियाँ हैं ।
04:36View SolutionFind the eccentricity of the hyperbola x2−y2=1. If S, S1 are the foci and P any point on this hyperbola, prove that, CP2=SP⋅S1P (C is the origin.)
05:59View SolutionIf S and S' are the foci and P be any point on the hyperbola x2−y2=a2 , prove that ¯¯¯¯¯SP⋅¯¯¯¯¯¯¯S'P=CP2 , where C is the centre of the hyperbola .
03:03View SolutionIf C is the centre of a hyperbola x2a2−y2b2=1 , S, S its foci and P a point on it. Prove tha SP. S'P =CP2−a2+b2
07:00View Solutionx2−y2=a2 সমপরাবৃত্তের কেন্দ্র C এবং দুটি নাভি S ও S', যদি সমপরাবৃত্তের ওপর P যে-কোনো বিন্দু হয়, তবে দেখাও যে, ¯¯¯¯¯SP⋅¯¯¯¯¯¯¯S’P=CP2।
04:23View Solutionx2−y2=1 পরাবৃত্তের উৎকেন্দ্রতা নির্ণয় করো। যদি পরাবৃত্তের দুটি নাভি S, S1এবং P তার উপর যেকোনো বিন্দু হয়, তবে প্রমাণ করো যে, CP2=¯¯¯¯¯SP⋅¯¯¯¯¯¯¯S1P (C-হল মূলবিন্দু)
02:19View SolutionIf S and T are foci of x216−y29=1. If P is a point on the hyperbola then |SP-PT|=
13:08View SolutionIf S ans S' are the foci, C is the center , and P is point on the rectangular hyperbola, show that SP×S'P=(CP)2
10:23View SolutionIf S, S' are the foci and' P any point on the rectangular hyperbolax2−y2=a2, prove that,¯¯¯¯¯SP.¯¯¯¯¯¯¯S'P=CP2 where C is the centre of the hyperbola
07:45View Solution