P(asecα,btanα) and Q(asecβ,btanβ) are two given points on the hyperbola x2a2−y2b2=1. Show that the equation of the chord PQ is
xacos(α−β)2−ybsin(α+β)2=cos(α+β)2.Solution in Bengali
Step by step video & image solution for P(asec alpha, b tan alpha) and Q(a sec beta, b tan beta) are two given points on the hyperbola (x^(2))/(a^(2))-(y^(2))/(b^(2)) = 1. Show that the equation of the chord PQ is (x)/(a) cos (alpha - beta)/(2) - (y)/(b) sin (alpha + beta)/(2) = cos (alpha+beta)/(2). by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - MULTIPLE CHOICE TYPE QUESTIONS
20 Videos
- HYPERBOLABOOK - CHHAYA PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - VERY SHOT ANSWER TYPE QUESTIONS
16 Videos
- DIAGRAMMATIC REPRESENTATION OF DATABOOK - CHHAYA PUBLICATIONCHAPTER - DIAGRAMMATIC REPRESENTATION OF DATAEXERCISE - EXERCISE (Very short Answer Type Question)
7 Videos
- MATHEMATICAL INDUCTION BOOK - CHHAYA PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION EXERCISE - Sample Questions for Competitive Exams
20 Videos
Similar Questions
If e is the eccentricity of the hyperbola x2a2−y2b2=1 , then e =
View SolutionExplain what geometrical diagrams are represented by the equatio x2a2+y2a2(1−e2)=1, where a and e are constants.
View SolutionThe following table gives the frequency distribution of heights in inches of a group of 100 peple:
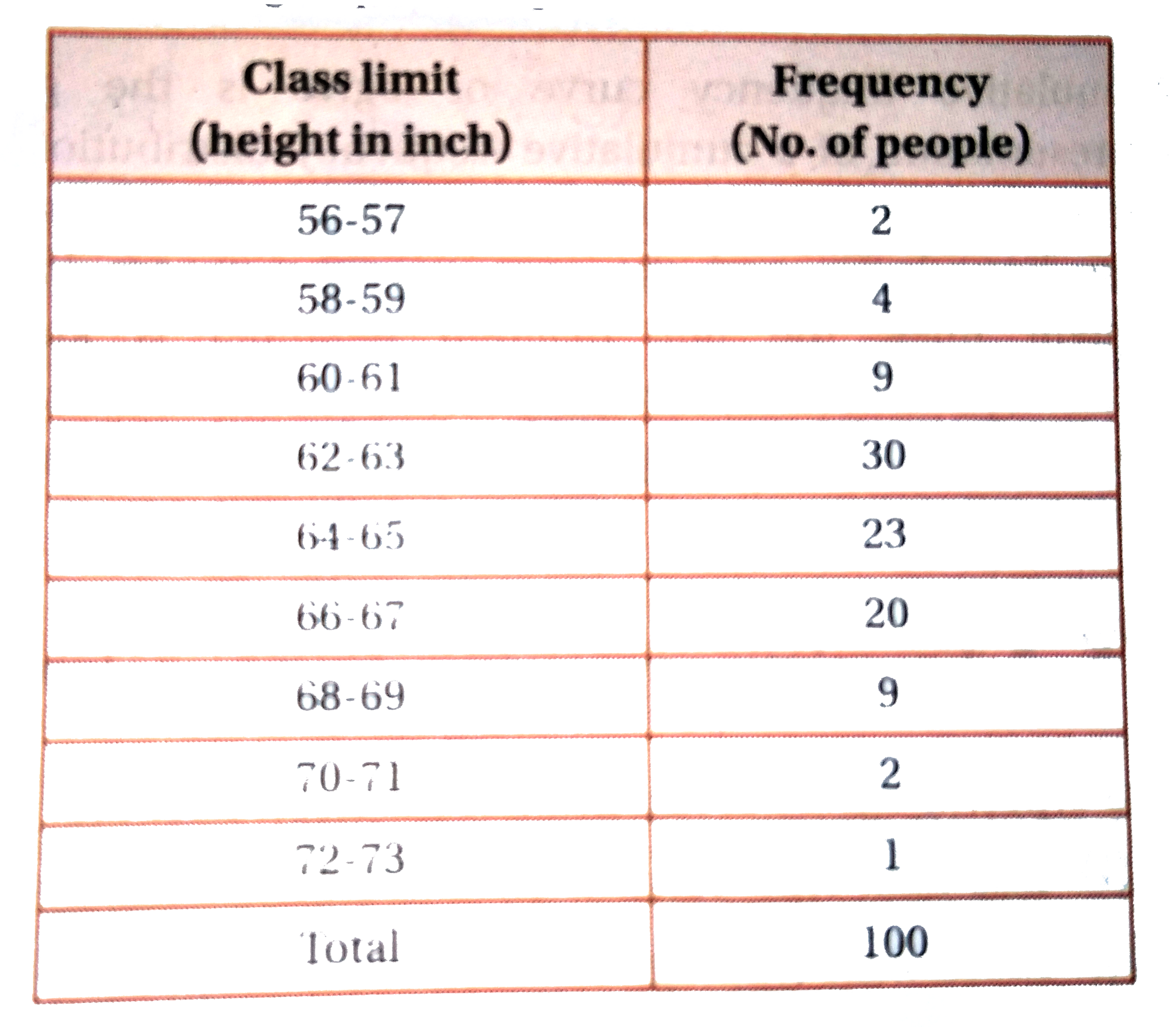 Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
Draw a histogram for height distribution. Shade the portion of the histogram which will represent the total number of people whose heights lie between 60.5 and 66.5 inches.
View SolutionIf for all n∈N and n≥1, then (32n−1) is always divisible by
View SolutionIf atanα+btanβ=(a+b)tan(α+β2) , where α≠β , prove that acosβ=bcosα.
View SolutionIf sinα+sinβ=a and cosα+cosβ=b then tan(α−β2) is equal to
View Solutiontan alpha and tan beta are roots of the equation x^(2)+ax+b=0, then the value of sin^(2)(alpha+beta)+a sin(alpha+beta)cos(alpha+beta)+b cos^(2)(alpha+beta) is equal to
View Solutiontan alpha and tan beta are roots of the equation x^(2)+ax+b=0, then the value of sin^(2)(alpha+beta)+a sin(alpha+beta)*cos(alpha+beta)+b cos^(2)(alpha+beta) is equal to
View SolutionIf sinα+sinβ=a and cosα−cosβ=b then tan(α−β2) is equal to-
View SolutionIf sin alpha+sin beta=a and cos alpha-cos beta=b then tan((alpha-beta)/(2))=
View SolutionIf (x) / (a) cos alpha + (y) / (b) sin alpha = 1, (x) / (a) cos beta + (y) / (b) sin beta = 1 and (cos alpha cos beta) / (a ^ (2)) + (without alpha without beta) / (b ^ (2)) = 0 then
View Solutionसाबित करें कि tan2α−tan2β=sin(α+β)sin(α−β)cos2αcos2β
View Solutionयदि sinα+sinβ=x तथा cosα+cosβ=y, तो सिद्ध कीजिय की tan(α+β)2=xy तथा cos(α−β2)=√x2+y22
View SolutionIfα≠β and atanα+btanβ=(a+b)tanα+β2,show thatcosαcosβ=ab.
View SolutionIfxcosα+ysinα=xcosβ+ysinβ,show that,y=xtanα+β2
View Solution
