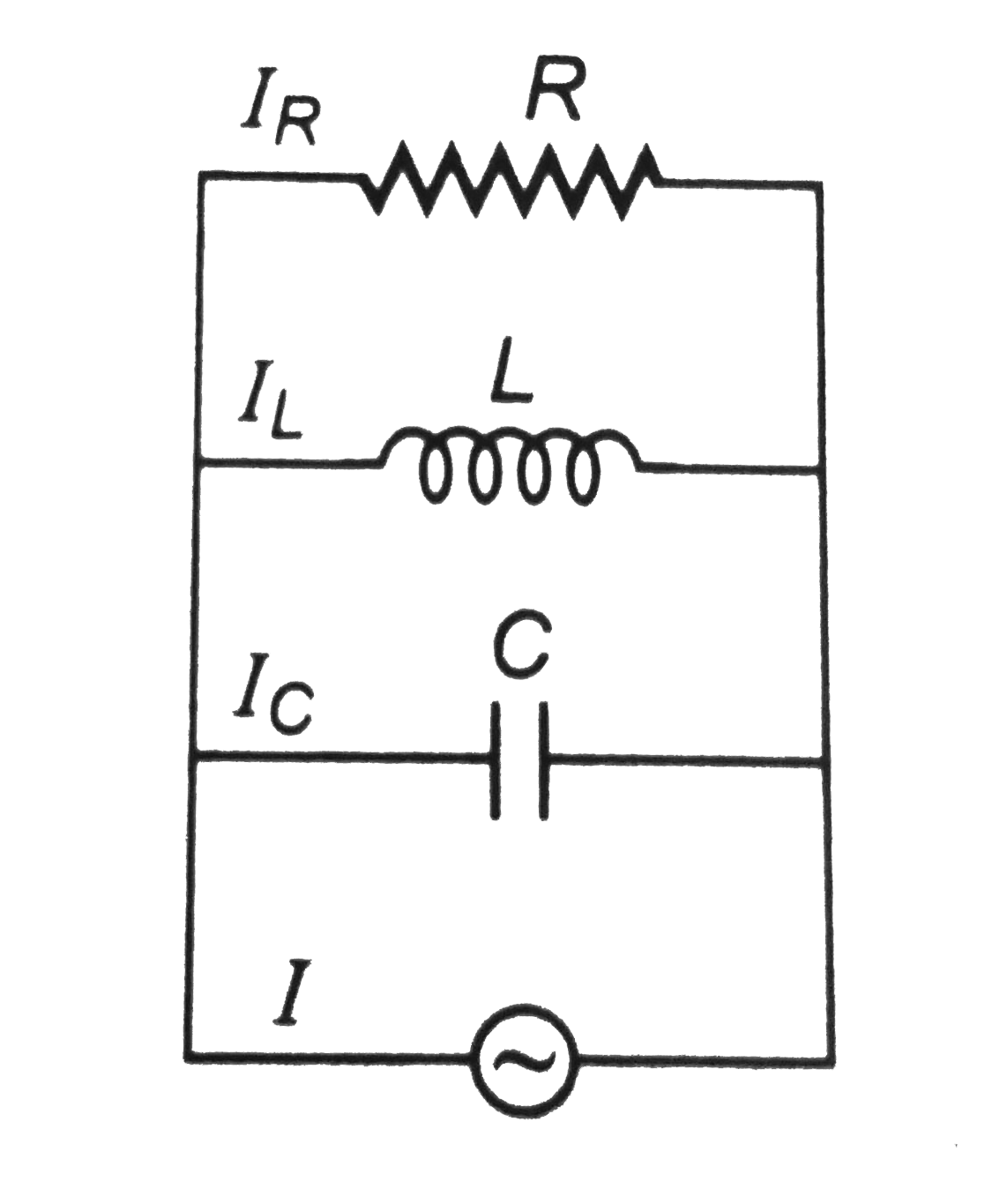
An AC source is connected in parallel with an L-C-R circuit as shown.Let denote the currents through and the voltage across the corresponding componts.Then,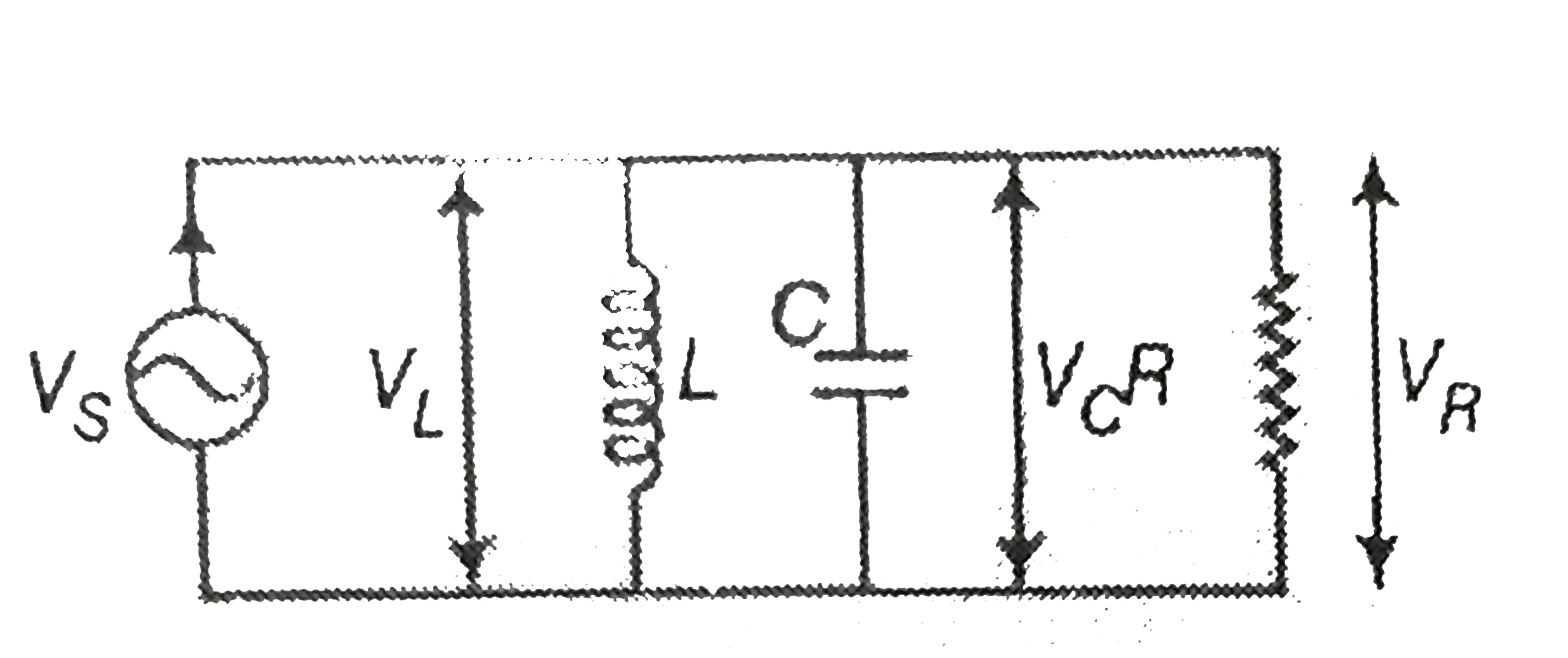
may be
The correct Answer is:D
Step by step video, text & image solution for An AC source is connected in parallel with an L-C-R circuit as shown.Let l_(s), l_(L), l_(C) " and " l_(R) denote the currents through and V_(s), V_(L), V_(C) " and "V_(R)the voltage across the corresponding componts.Then, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
An AC source is connected in parallel with an L-C-R circuit as shown. Let IS,IL,IC and IR denote the currents through and VS,VL,VC and VR the voltages across the corresponding components. Then,
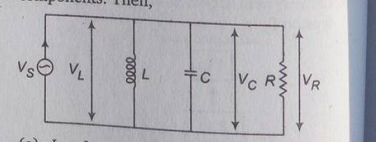 AIS=IL+IC+IRBVS=VL+VC+VRC(IL,IC,IR)<ISDIL,IC may be greater than IS
AIS=IL+IC+IRBVS=VL+VC+VRC(IL,IC,IR)<ISDIL,IC may be greater than ISAn AC source is connected in parallel with an L-C-R circuit as shown. Let IS,IL,IC and IR denote the currents through and VS,VL,VC and VR the voltages across the corresponding components. Then,
 AIS=IL+IC+IRBVS=VL+VC+VRC(IL,IC,IR)<ISDIL,IC may be greater than IS
AIS=IL+IC+IRBVS=VL+VC+VRC(IL,IC,IR)<ISDIL,IC may be greater than ISIn an LCR series ac circuit the voltage across L,C and R are V1,V2 and V3 respectively The voltage of the source is .
A√(V1−V2)2+V23B√V21+(V2−V23C√V22+(V1−V3)2DV1+V2+V3
The current growth in two L-R circuits (b) and (c) is as shown in Fig. Let L1,L2,R1andR2 be the corresponding values in two circuits. Then
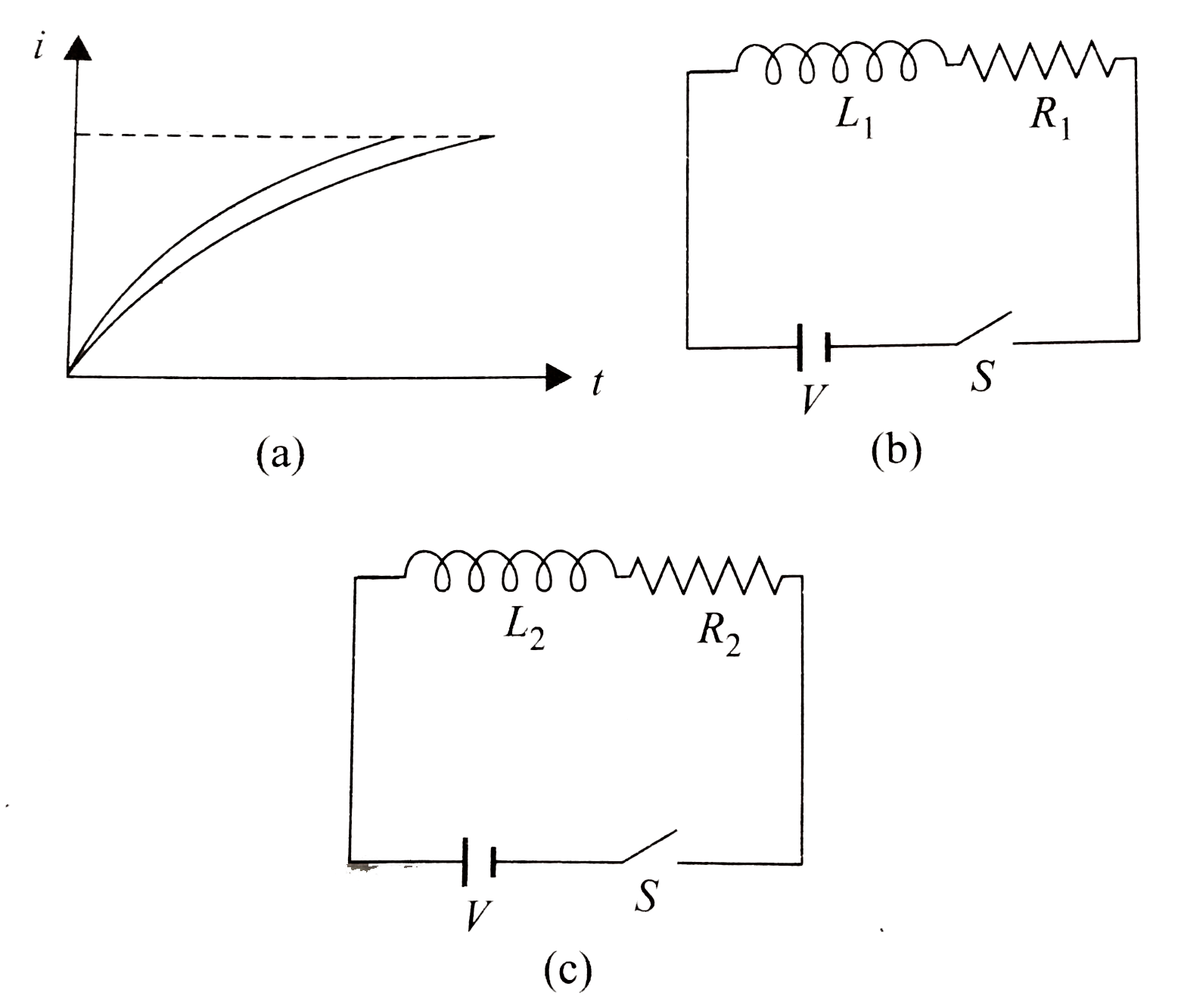
View SolutionCurrent growth in two L-R circuits (b) and (c ) as shown in figure (a). Let L1,L2,R1 and R1 be the corresponding values in two circuits. Then
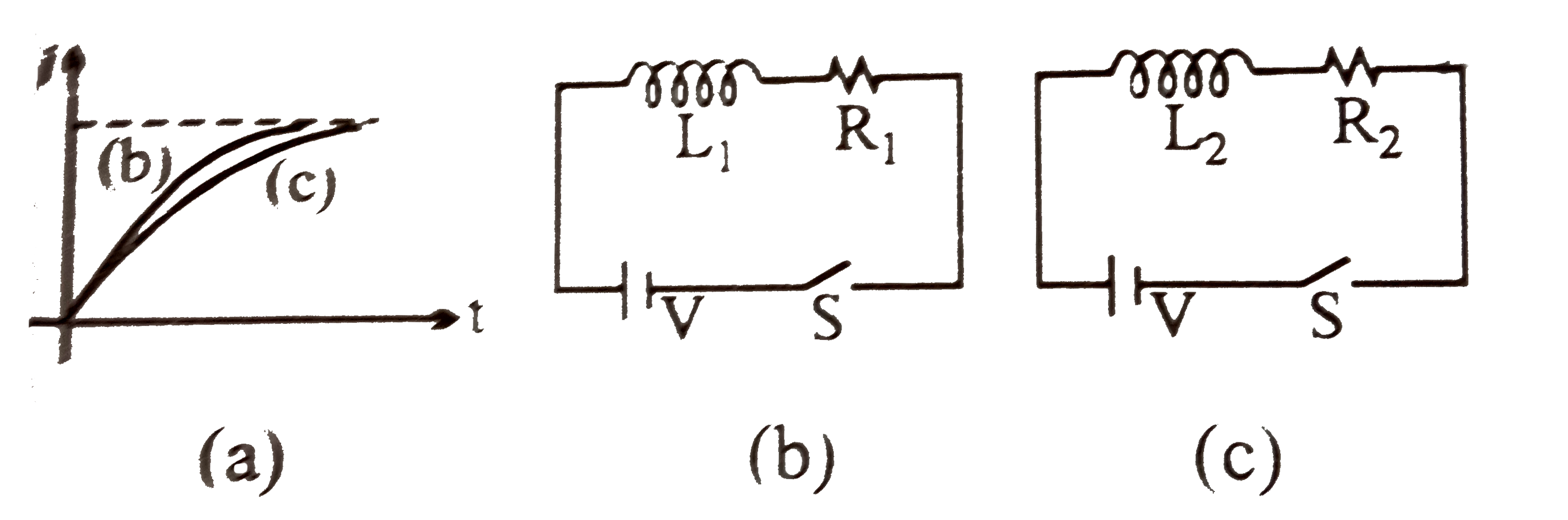
View SolutionIn a parallel L−C−R circuit as shown in figureure if IR,IL,IC and I represent the rms values of current flowing through resistor, capacitor and the source, then choose the appropriate correct answer.
 .
.
View SolutionIn an LCR circuit, the voltages across the components are VL,VC and VR respectively. The voltage of source will be -
View SolutionFigures shows a parallel LCR circuit connected to a 200V, AC source. L=5H, C=80μFandR=40Ω. At resonance let I1andi2 be the rs currents through L,C and R. Then

View Solution

