A charge q coulomb moves in a circle at n revolution per second and the radius of the circle is r metre. Then magnetic feild at the centre of the circle is

$\frac{2 π q}{n r} \times 10^{- 7} N / A m$

$\frac{2 π n q}{r} \times 10^{- 7} N / A m$

$\frac{2 π q}{n r} N / A m$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

An infinitely long conductor is bent into a circle as shown in figure. It carries a current I ampere and the radius of loop is R meter. The magnetic induction at the centre of loop is

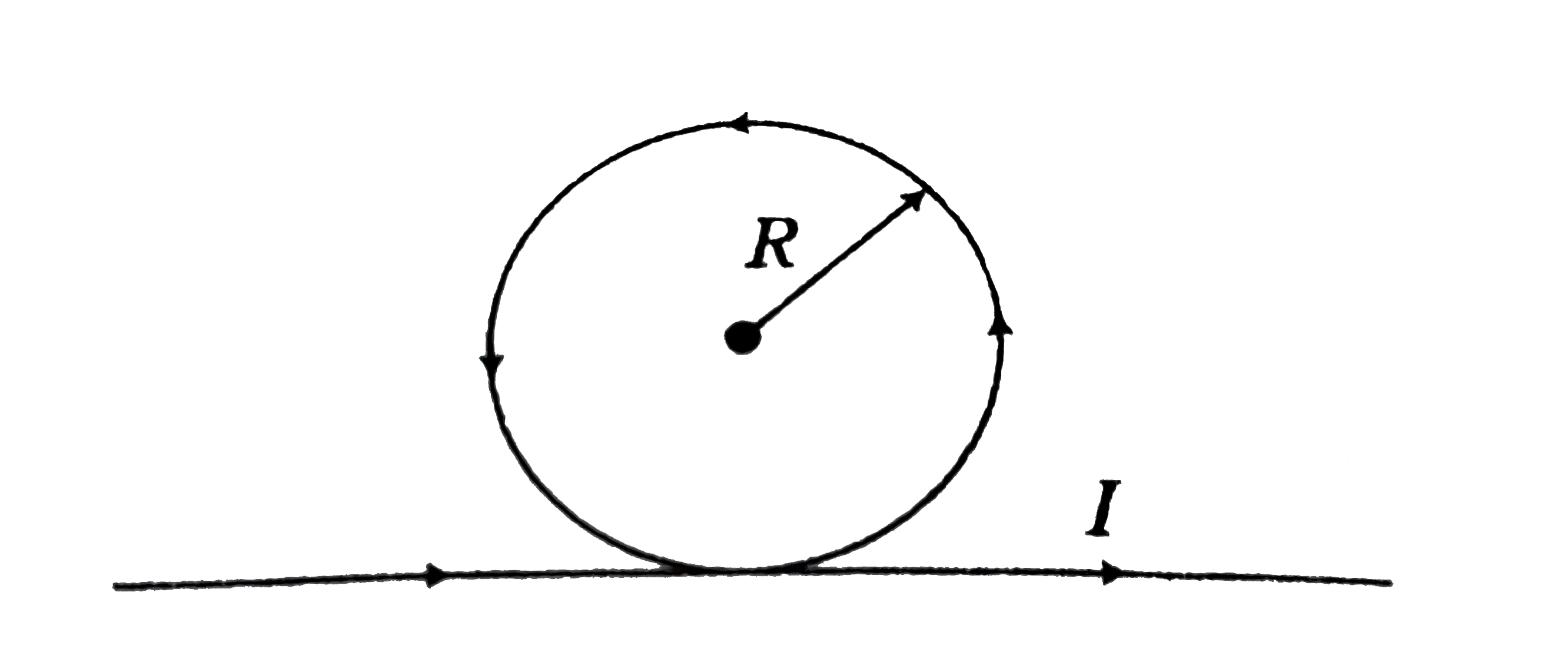A $\frac{μ_{0} 2 I}{4 π R} (π + 1)$
B $\frac{μ_{0} 2 I}{4 π R} (π - 1)$
C $\frac{μ_{0} I}{8 π R} (π + 1)$
Dzero
A charge of $10^{- 6} C$ is describing a circular path of radius 1cm making 5 revolution per second. The magnetic induction field at the centre of the circle is
A $π \times 10^{- 10} T$
B $π \times 10^{- 9} T$
C $\frac{π}{2} \times 10^{- 10} T$
D $\frac{π}{2} \times 10^{- 9} T$
In total, 10 charges (5 of them are $+ q$ each and other 5 are $- q$ each) are placed randomly on the circumference of a circle. The radius of the circle is R. The electric potential at the center of this circle due to these charges will be
A $0$
B $10 K q / R$
C $5 K q / R$
DCannot be calculated unless the positions of the charges on the circle are specified.