The capacitance of earth of radius R treating as spherical conductor is
4π∈0R
4πR
∈0R
4π∈0R
The correct Answer is:A
To find the capacitance of the Earth, treating it as a spherical conductor, we can follow these steps:
Step 1: Understand the Concept of Capacitance for a Spherical Conductor
The capacitance C of a spherical conductor can be derived from the general formula for spherical capacitors. For a spherical conductor with radius r, the capacitance is given by the formula:
C=4πϵ01A−1B
where A is the inner radius and B is the outer radius.
Step 2: Define the Radii for the Earth
In this case, we treat the Earth as a solid sphere of radius r. We can consider the outer radius B to be at infinity, which simplifies our calculations. Thus, we have:
- Inner radius A=r
- Outer radius B=∞
Step 3: Substitute the Values into the Capacitance Formula
Now, substituting the values into the capacitance formula:
C=4πϵ01r−1∞
Since 1∞=0, the formula simplifies to:
C=4πϵ01r=4πϵ0r
Step 4: Final Expression for the Capacitance
Thus, the capacitance of the Earth, treating it as a spherical conductor, is:
C=4πϵ0r
Step 5: Conclusion
This formula indicates that the capacitance of the Earth depends directly on its radius r and the permittivity of free space ϵ0.
The capacitance C of a spherical conductor can be derived from the general formula for spherical capacitors. For a spherical conductor with radius r, the capacitance is given by the formula:
In this case, we treat the Earth as a solid sphere of radius r. We can consider the outer radius B to be at infinity, which simplifies our calculations. Thus, we have:
- Outer radius B=∞
Now, substituting the values into the capacitance formula:
Thus, the capacitance of the Earth, treating it as a spherical conductor, is:
This formula indicates that the capacitance of the Earth depends directly on its radius r and the permittivity of free space ϵ0.
Topper's Solved these Questions
Similar Questions
Find out the capacitance of an isolated spherical conductor of radius R
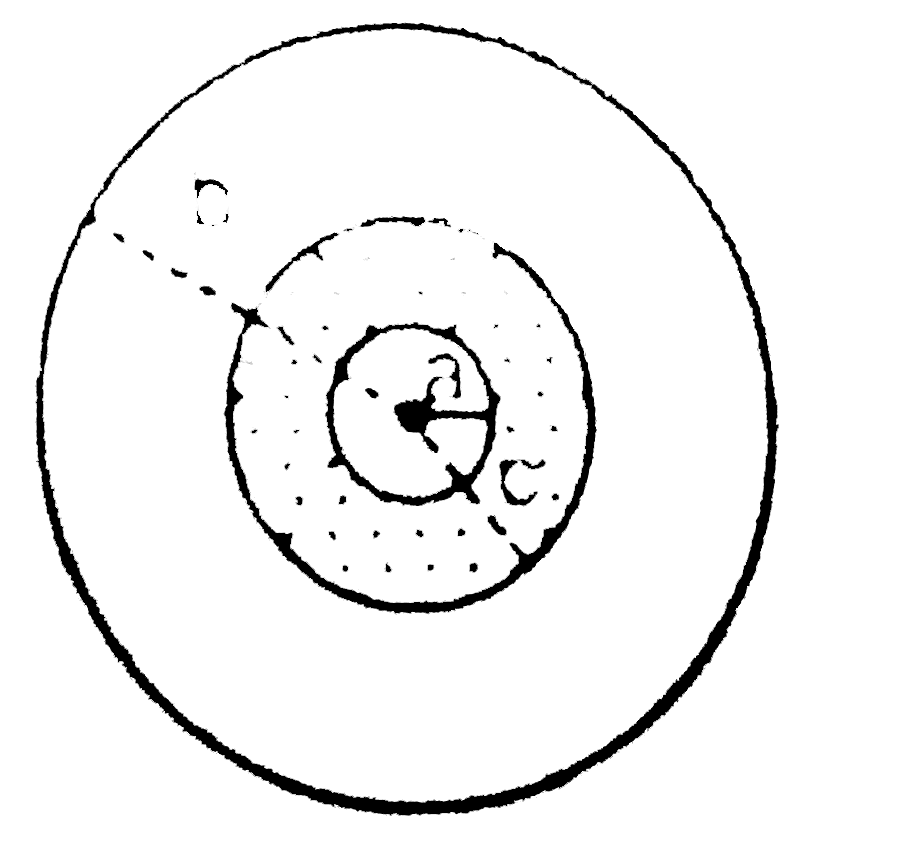
View SolutionA spherical capacitor is made of two conducting spherical shells of radii a and b = 3a . The space between the shells is filled with a dielectric of dielectric constant K = 3 upto a radius c = 2a as shown. If the capacitance of given arrangement is n times the capacitance of an isolated of an isolated spherical conducting shell of radius a. Then find value of n .
View Solution
Knowledge Check
The capacitance of earth, treating it as a spherical conductor of radius 6400 km is
A5.1×10−4FB6.1×10−4FC7.1×104FD7.1×10−4FThe capacitance of the earth, viewed as a spherical conductor of radius 6408 km is
A980μFB1424μFC712μFD356μFThe capacity of a spherical conductor is
AR4πε0B4πε0RC4πε0RD4πε0R2
A parallel-plate capacitor has each plate of 6 cm diamter. If its two plates are separated by 0.05 cm of air, what should be the capacitance of the capacitor? What would be the radius of a spherical conductor having the same capacitance?
View SolutionShow that the capacitance of an insulated spherical conductor is directly proportional to the radius of the conductor.
View SolutionFind the capacitance of an isolated spherical conductor of radius a surrounded by a concentric layer of dielectric of outer radius b and relative permittivity. ε
View SolutionThe capacitance of a conductor ____________ when an earthed conductor is brought near it.
View SolutionWhat is the capacitance of a spherical conductor with radius 1 m?
View Solution

