In Young's experiment, monochromatic light is used to illuminate the two slits A and B. Interference fringes are observed on a screen placed in front of the slits. Now if a thin glass plate is placed normally in the path of the beam coming from the slit
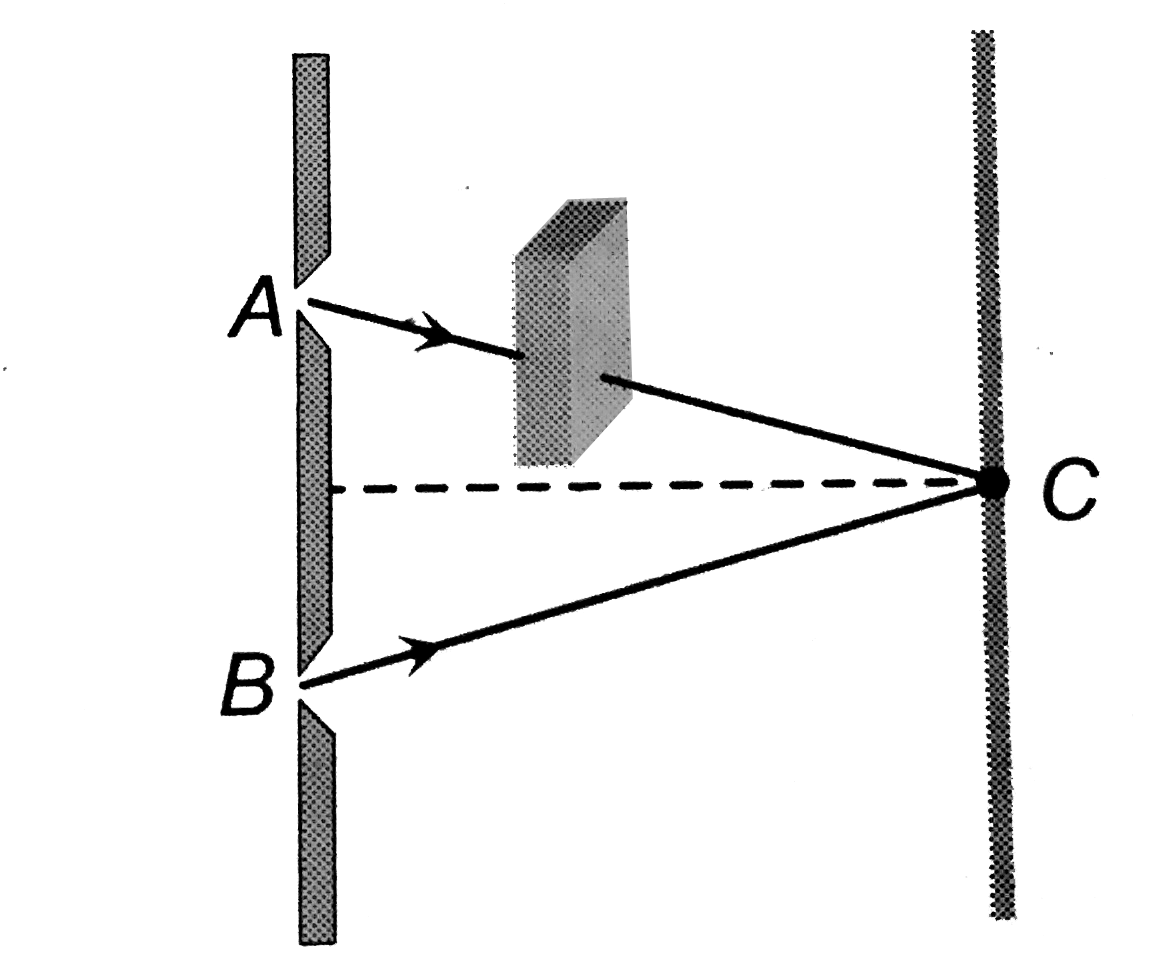
fringes will disappear
the fringe width will dicreases
the fringe width will increases
there will be no changed in the fringe width
The correct Answer is:D
By introduction of slab in the path of one interfering beam, the entire, interference pattern is shifted in the direction of slab, but fringe width remains unchanged
Topper's Solved these Questions
Similar Questions
In Young's double slit experiment , red light of wavelength 620 nm is used and the two slits are 0.3 mm apart . Interference fringes are observed on a screen 1.3 mm apart . Calculate (i) the distance of slits from the screen and (ii) the fringe width if this distance is doubled .
View SolutionIn Young's double-slit experiment , the slits are 0.5 mm apart and interference is observed on a screen placed at 1.0 m from the slits. It is found that the 9th bright fringe is at 8.835 mm from the 2nd dark fringe on the same side of the interference pattern. Find the wavelength of light used.
View Solution
Knowledge Check
In Young’s experiment, monochromatic light through a single slit S is used to illuminate the two slits S1and S2. Interference fringes are obtained on a screen. The fringe width is found to be w. Now a thin sheet of mica (thickness t and refractive index μ) is placed near and in front of one of the two slits. Now the fringe width is found to be w’, then :
Aw'=w/μBw'=wμCw'=(μ−1)twDw'=wA two slit Young's interference experiment it done with monochromatic light of wavelength 6000A. The slits are 2mm apart. The fringes are observed on a screen placed 10cm away from the slits. Now a transparent plate of thickness 0.5mm is placed in front of one of the slits and it if found that the interference pattern shifts by 5mm. The refractive index of the transparent plate is :
A1.2B0.6C2.4D1.5A Young's double slit experiment uses a monochromatic source. The shape of the interference fringes formed on a screen is
A(a) Straight lineB(b) ParabolaC(c) HyperbolaD(d) Circle
In Young's double slit experiment the slits are 0.5 mm apart and interference is observed on a screen placed at a distance of 100 cm from the slits. It is found that the 9th bright fringe is at a distance of 8.835 mm from the second dark fringe from the centre of the fringe pattern. Find the wavelength of light used.
View SolutionIn Young's double slit experiment, if the two slits are illuminated with separate sources, no interference pattern is observed because
View SolutionIn a Young's double-slit experiment, green light is incident on the two slits. The interference pattern is observed on a screen. Which one of the following changes would cause the observed fringes to be more closely spaced?
View SolutionIn Young's double slit experiment, the two slits are at a distance 'd' apart. Interference pattern is observed on a screen at a distance D front the slit, if at a point on the screen, directly opposite to the slits, the first dark fringe is observed, then wave length of the wave will be
View Solution_E01_055_Q01.png)
In a young's double slit experiment, green light is incident on the two slits. The interference pattern is observed on a screen. Which of the following changes would cause the observed fringes to be more closely spaced?
View Solution

