Two waves at a point are represented by E(1)= E(0) sin omega t and E(2

If $i_{1} = i_{0} sin (ω t), i_{2} = i_{0_{2}} sin (ω t + ϕ)$ , then $i_{3} =$

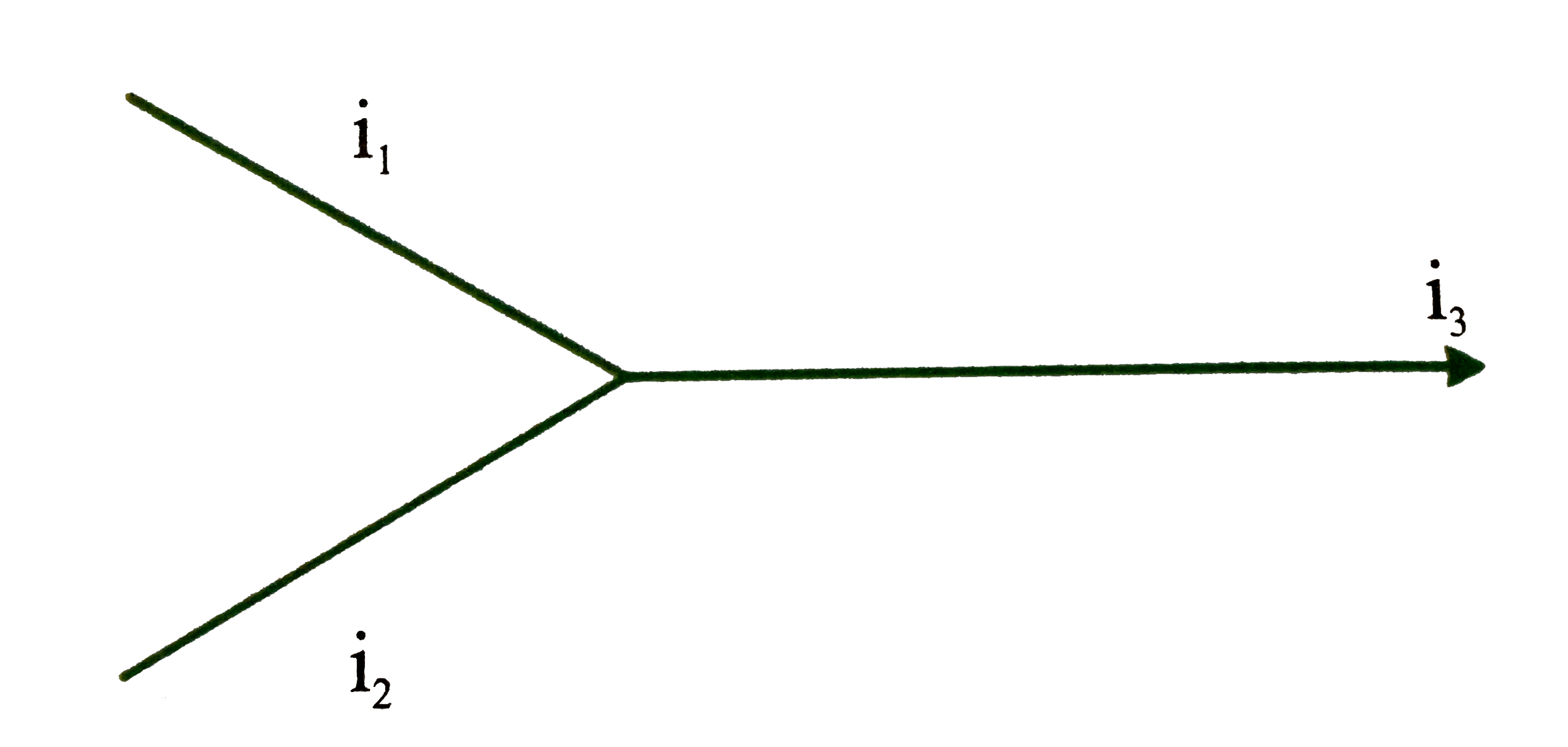A $\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2}} sin {ϕ + ω t}$
B $(i_{0_{1}} + i_{0_{2}}) sin (\frac{ϕ}{2} + ω t)$
C $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [ϕ + ω t]$
D $(\sqrt{i_{0_{1}}^{2} + i_{0_{2}}^{2} + 2 i_{0_{1}} i_{0_{2}} cos ϕ}) sin [α + ω t]$ where $α = {Tan}^{- 1} [\frac{i_{0_{2}} sin ϕ}{i_{0_{1}} + i_{0_{2}} cos ϕ}]$
Two wave are represented by equation $y_{1} = a sin ω t$ and $y_{2} = a cos ω t$ the first wave :-
Aleads the second by $π$
Blags the second by $π$
Cleads the second by $\frac{π}{2}$
Dlags the second by $\frac{π}{2}$
Two coherent waves are represented by $y_{1} = a_{1} {cos}_{ω}$ t and $y_{2} = a_{2} {sin}_{ω}$ t. The resultant intensity due to interference will be
A $(a_{1}^{2} - a_{2}^{2})$
B $(a_{1}^{2} + a_{2}^{2})$
C $(a_{1} - a_{2})$
D $(a_{1} + a_{2})$

Two waves at a point are represented by $E_{1} = E_{0} sin ω t and E_{2} = E_{0} sin (ω + ϕ)$ . There will eb destructive interference at this point is