The amount of thermal radiations emitted from one square metre area of a black body in one second when at a temperature of 100 K is
5.67 J
56.7 J
567 J
5670 J
The correct Answer is:A
dQdtA=σT4
Topper's Solved these Questions
- KINETIC THEORY OF GASES & RADIATION BOOK - NIKITA PUBLICATIONCHAPTER - KINETIC THEORY OF GASES & RADIATION EXERCISE - MCQs (Newtons Law of Cooling)
40 Videos
- KINETIC THEORY OF GASES & RADIATION BOOK - NIKITA PUBLICATIONCHAPTER - KINETIC THEORY OF GASES & RADIATION EXERCISE - MCQs (Question Given in MHT-CET)
79 Videos
- KINETIC THEORY OF GASES & RADIATION BOOK - NIKITA PUBLICATIONCHAPTER - KINETIC THEORY OF GASES & RADIATION EXERCISE - MCQs (Kirchhoffs law of heat radiation)
19 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - NIKITA PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - MULTPLE CHOICE QUESTIONS
333 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENTBOOK - NIKITA PUBLICATIONCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENTEXERCISE - MCQs (Sensitivity and accuracy of M.C.G.)
1 Videos
Similar Questions
Knowledge Check
The amount of thermal radiations emitted from one square centimetre area of a black body in one second when at a temperature of 1000 K is:
A5.67 JB56.7 JC567 JD5670 JWhich of the following graphs correctly represents the relation between In (E) and In (T), where E is the amount of radiation emitted per unit time from a unit area of the body and T is the absolute temperature ?
A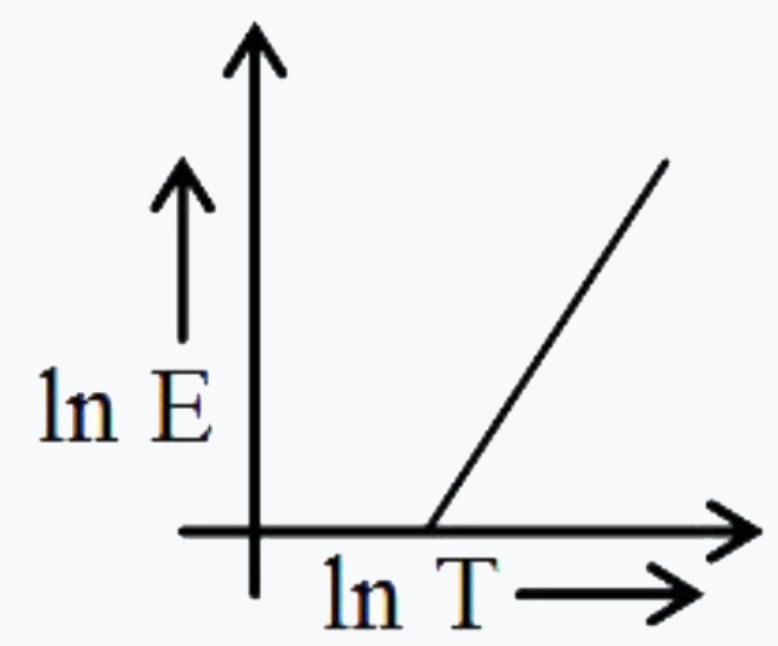 B
B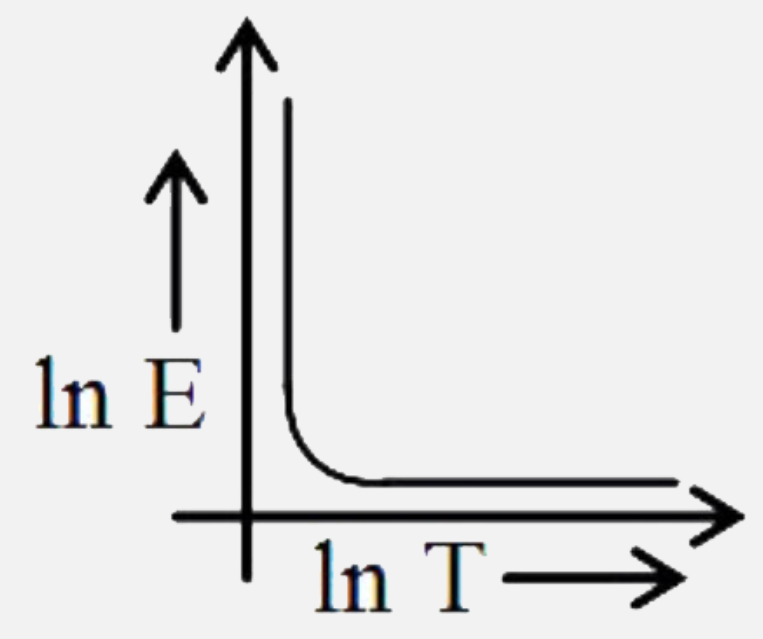 C
C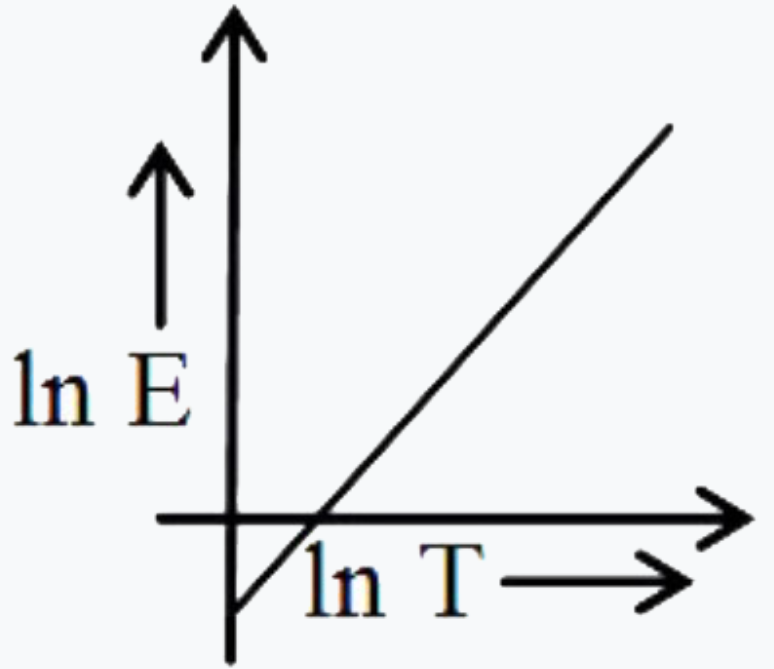 D
D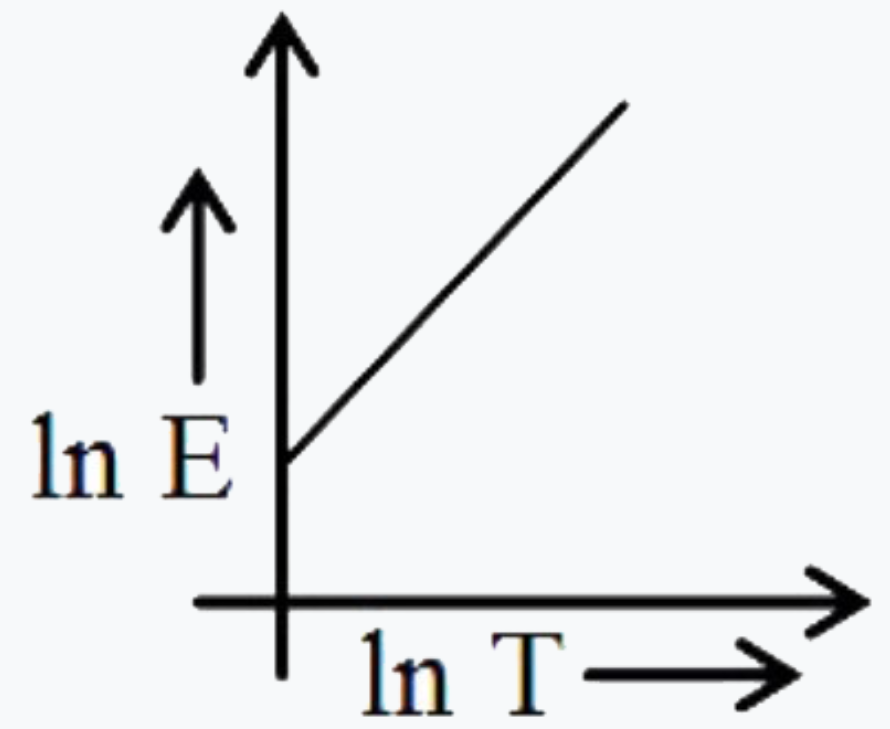
The amount of radiations emitted per second by unit area of a hollow container at 103∘ K will be-
A567 JB5670 JC56700 JD567000 J
In the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
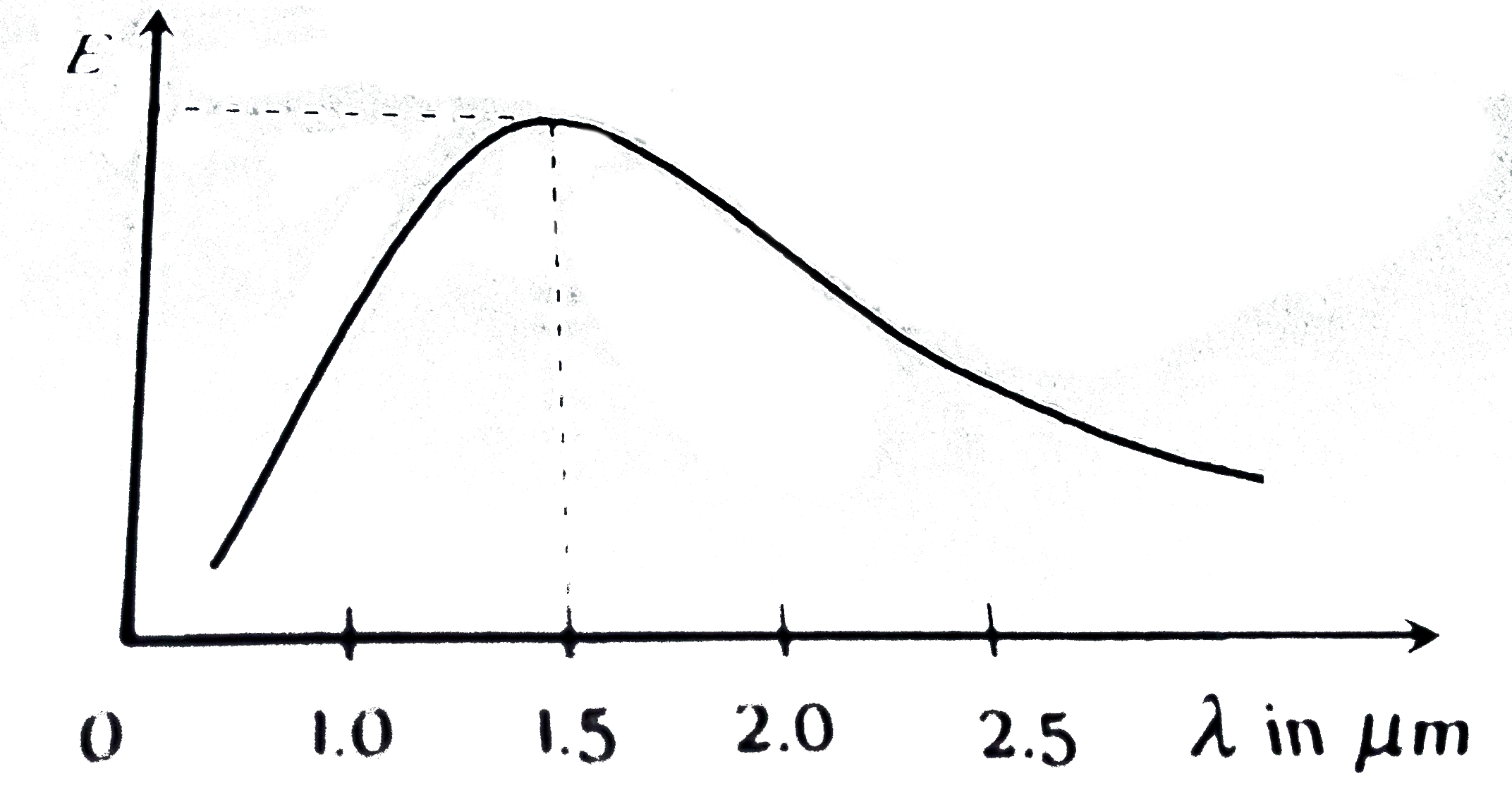
View SolutionThe rate at which a black body emits radiation at a temperature T is proportional to
View SolutionThe rate at which a black body emits radiation at a temperature T is proportional to
View SolutionSolar radiation emitted by the sun resembles the radiations emitted by a black body at the temprature of 6000 K. Maximum intensity is emitted at a wavelength of 4800 Å. If the temperature of the sun decreases from 6000 K to 4000 K , then the peak intensity would occur at a wavelength of
View SolutionThe ratio of energies of emitted radiation by a black body at 600 K and 900 K , when the surrounding temperature is 300 K , is
View Solution
