An automobile moving at 30 m/s is approaching a factory whistle that has a frequency of 500 Hz. If the speed of the sound in air is 340 m/s, then the apparent frequency of the whistle as heard by the driver is
456 Hz
544 Hz
500 Hz
597 Hz
The correct Answer is:B
To find the apparent frequency of the whistle as heard by the driver of the automobile, we can use the Doppler effect formula for a stationary source and a moving observer. The formula is:
f′=f(v+vov)
Where:
- f′ is the apparent frequency,
- f is the actual frequency of the source,
- v is the speed of sound in air,
- vo is the speed of the observer (the automobile in this case).
1. Identify the given values:
- Frequency of the whistle, f=500Hz
- Speed of sound in air, v=340m/s
- Speed of the observer (automobile), vo=30m/s
2. Substitute the values into the Doppler effect formula:
f′=500(340+30340)
3. Calculate the numerator:
340+30=370m/s
4. Now substitute back into the formula:
f′=500(370340)
5. Calculate the fraction:
370340≈1.0882
6. Now multiply by the original frequency:
f′≈500×1.0882≈544.1Hz
7. Round to the appropriate significant figures:
f′≈544Hz
Final Answer:
The apparent frequency of the whistle as heard by the driver is approximately 544 Hz.
- f′ is the apparent frequency,
- f is the actual frequency of the source,
- v is the speed of sound in air,
- vo is the speed of the observer (the automobile in this case).
- Frequency of the whistle, f=500Hz
- Speed of sound in air, v=340m/s
- Speed of the observer (automobile), vo=30m/s
f′=500(340+30340)
340+30=370m/s
f′=500(370340)
370340≈1.0882
f′≈500×1.0882≈544.1Hz
f′≈544Hz
The apparent frequency of the whistle as heard by the driver is approximately 544 Hz.
Topper's Solved these Questions
Similar Questions
A person is standing on a platform. As engine while approaching the platform blows a whistle , the frequency of which is 100 Hz.The speed of engine is 108kmh−1 and speed of sound is 340ms−1.Calculate the appearent frequency of the whistle as heard by the person.
View SolutionThe driver of a car travelling with speed 30ms−1 towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330ms−1, the frequency of reflected sound as heard by driver is
View Solution
Knowledge Check
The driver of a car travelling with a speed of 30 m/s towards a wall sounds a siren of frequency 500 Hz. If the velocity of sound in air is 330 m/s, then the frequency of the sound reflected from the wall and as heard by the driver is
A550 HzB600 HzC650 HzD450 HzA train moving at 40 m/s, passes by a stationary observer, emitting a whistle of frequency 300 Hz. If the velocity of sound wave is 340 m/s, then the change in the apparent frequency of the sound, just before and after the train passes by the observer will be nearly
A32 HzB72 HzC40 HzD8 HzA whistle whose air column is open at both ends has a fundamental frequency of 5100 Hz. If the speed of sound in air is 340 ms−1, the length of the whistle, in cm, is
A5/3B10/3C5D20/3
The driver of a car travelling with speed 30ms−1 towards a hill sounds a horn of frequency 600 Hz. If the velocity of sound in air is 330ms−1, the frequency of reflected sound as heard by driver is
View SolutionA train is moving with a uniform speed of 33 m/s and an observer is approaching the train with the same speed. If the train blows a whistle of frequency 1000 Hz and the velocity of sound is 333 m/s, then the apparent frequency of the sound that the observer hears is
View SolutionA car moving at 35 m/s approaches a stationary whistle that emits a 220 Hz sound. The speed of sound is 343 m/s. What is the speed of the sound relative to the driver of the car?
View Solution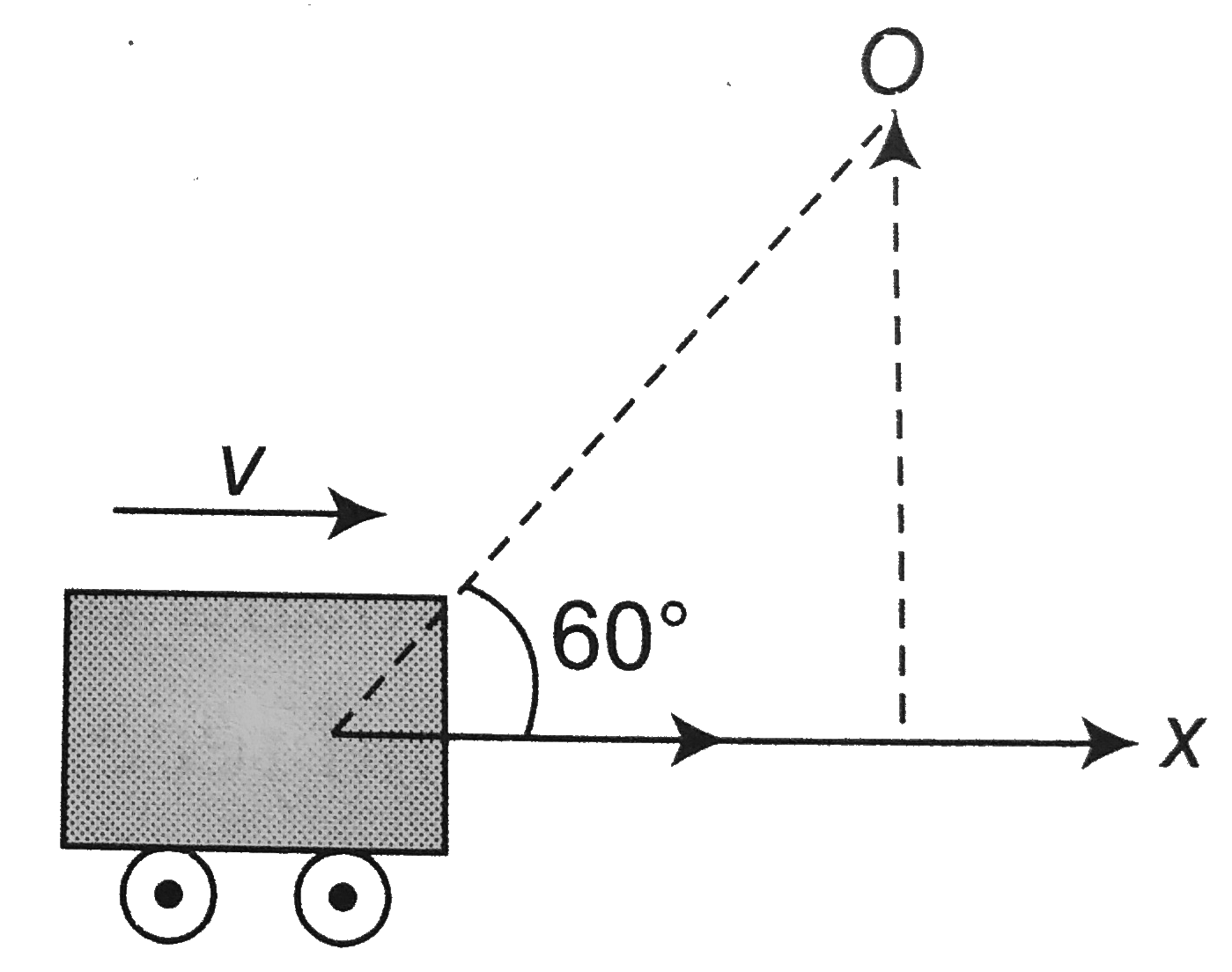
A car is moving along X-axis with a velocity v=20m/s. It sounds a whistle of frequency 660 Hz. If the speed of sound is 340m/s. The apparent frequency heard by the observer O (shown in figure) is:
View SolutionA car, sounding a horn of frequency 1000 Hz, is moving directly towards a huge wall at a speed of 15 m/s. If speed of sound is 340 m/s, then the frequency of the echo heard by the driver is
View Solution
