A soap film of surface tension $3 \times 10^{- 2} N / m$ formed in a rectangular frame can support a straw as shown in Fig. If $g = 10 m s^{- 2}$ , the mass of the straw is

$0.66$ g

60 g

6 g

$0.6$ g

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

A soap film of surface tension $3 \times 10^{- 2}$ formed in a rectangular frame can support a straw as shown in Fig. If $g = 10 m s^{- 12}$ , the mass of the straw is

A $0.006 g$
B $0.06 g$
C $0.6 g$
D $6 g$
A circular wire of length 0.1 m is touching the surface of the liquid of surface tension $3 \times 10^{- 2}$ N/m The mass of a wire is $10^{- 4}$ kg . If g = 10 $m / s^{2}$ then the force needed to lift the circular wire is
A $7 \times 10^{- 3}$ N
B $0.7 \times 10^{- 3}$ N
C $0.07 \times 10^{- 3}$ N
D $70 \times 10^{- 3}$ N
In the arrangement as shown, tension $T_{2}$ is -
$(g = 10 m / s^{2})$

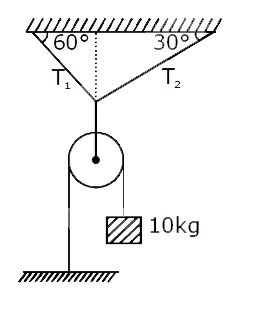A50 N
B100 N
C $50 \sqrt{3} N$
D $100 \sqrt{3} N$