Two springs of equal lengths and equal cross sectional area are made of materials whose young's moduli are in the ratio of 3 : 2. They are suspended and loaded with the same mass. When stretched and released, they will oscillate with time period in the ratio of
√2:√3
√3:√2
3:2
9:4
The correct Answer is:A
To solve the problem of finding the ratio of the time periods of oscillation of two springs made of materials with different Young's moduli, we can follow these steps:
Step 1: Understand the relationship between Young's modulus and spring constant
The spring constant k of a spring is related to the Young's modulus Y of the material, the cross-sectional area A, and the length L of the spring by the formula:
k=Y⋅AL
Since both springs have the same length and cross-sectional area, the spring constants can be expressed as:
kA=YA⋅ALandkB=YB⋅AL
Step 2: Find the ratio of the spring constants
Given the ratio of Young's moduli YAYB=32, we can express the spring constants in terms of this ratio:
kAkB=YAYB=32
Step 3: Relate the time period to the spring constant
The time period T of oscillation for a mass m attached to a spring is given by:
T=2π√mk
Thus, the time periods for the two springs can be expressed as:
TA=2π√mkAandTB=2π√mkB
Step 4: Find the ratio of the time periods
To find the ratio of the time periods, we take the ratio TATB:
TATB=2π√mkA2π√mkB=√kBkA
Substituting the ratio of the spring constants:
TATB=√23
Step 5: Finalize the answer
Thus, the ratio of the time periods TA:TB is:
TA:TB=√23:1
The spring constant k of a spring is related to the Young's modulus Y of the material, the cross-sectional area A, and the length L of the spring by the formula:
k=Y⋅AL
Since both springs have the same length and cross-sectional area, the spring constants can be expressed as:
kA=YA⋅ALandkB=YB⋅AL
Given the ratio of Young's moduli YAYB=32, we can express the spring constants in terms of this ratio:
kAkB=YAYB=32
The time period T of oscillation for a mass m attached to a spring is given by:
T=2π√mk
Thus, the time periods for the two springs can be expressed as:
TA=2π√mkAandTB=2π√mkB
To find the ratio of the time periods, we take the ratio TATB:
TATB=2π√mkA2π√mkB=√kBkA
Substituting the ratio of the spring constants:
TATB=√23
Thus, the ratio of the time periods TA:TB is:
TA:TB=√23:1
Topper's Solved these Questions
Similar Questions
Two springs of equal lengths and equal cross-sectional area are made of materials whose Young's moduli are in the ration of 2:3 . They are suspended and loaded with the same mass. When stretched and released they oscillate. Find the ratio of the time period of oscillation.
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View Solution
Knowledge Check
The young modulii of two springs of equal length and equal cross sectional areas are in the ratio 2:3 both the springs are suspended and loaded with the same mass . When springs are stretched and released , the time period of oscillation of the two springs is in the ratio of
A3:2B2:3C√3:√2D√2:√3Two light springs of same length and same area of cross section are made of materials whose young's modulii of elasticity are in the ratio 1 : 2. When loads of same mass are attached to the two springs, the ratio of their respectively time periods of oscillations is
A√2:1B1:√2C1:2D2:1A wire of length L and cross-sectional area A is made of material of Young's modulus Y. The work done in stretching the wire by an amount x is
AYAx2LBYAx22LC2YAx2LD4YAx2L
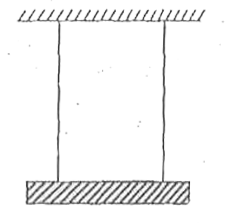
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
View SolutionA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
View SolutionA wire of length L and cross sectional area A is made of a material of Young's modulus Y. If the wire is stretched by an amount x, the work done is :
View SolutionA wire of length L and area of cross section A is made of a material of Young's modulus Y. If it is stretched by an amount x, the work done is given by
View SolutionTwo wires A and B have the same cross section and are made of the same material, but the length of wire A is twice that of B. Then, for a given load
View Solution
