When the displacement of a particle in SHM from the mean position is 4 cm, the force acting on the particle is 6 N. Then the force acting on it when its displacement is 6 cm from the mean positio is
3 N
16 N
8 N
9 N
The correct Answer is:D
Step by step video, text & image solution for When the displacement of a particle in SHM from the mean position is 4 cm, the force acting on the particle is 6 N. Then the force acting on it when its displacement is 6 cm from the mean positio is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
A body of mass 0.1 kg performing linear SHM experiences a restoring force of 1 N when its displacement from the mean position is 5 cm. Find (i) the force constant (ii) the period of SHM (iii) the acceleration of the body, when its displacement from the mean position is 1 cm./
View SolutionThe velocity of a particle in simple harmonic motion at displacement y from mean position is
View SolutionThe displacement time curve of a particle is shown in the figure. The external force acting on the particle is :
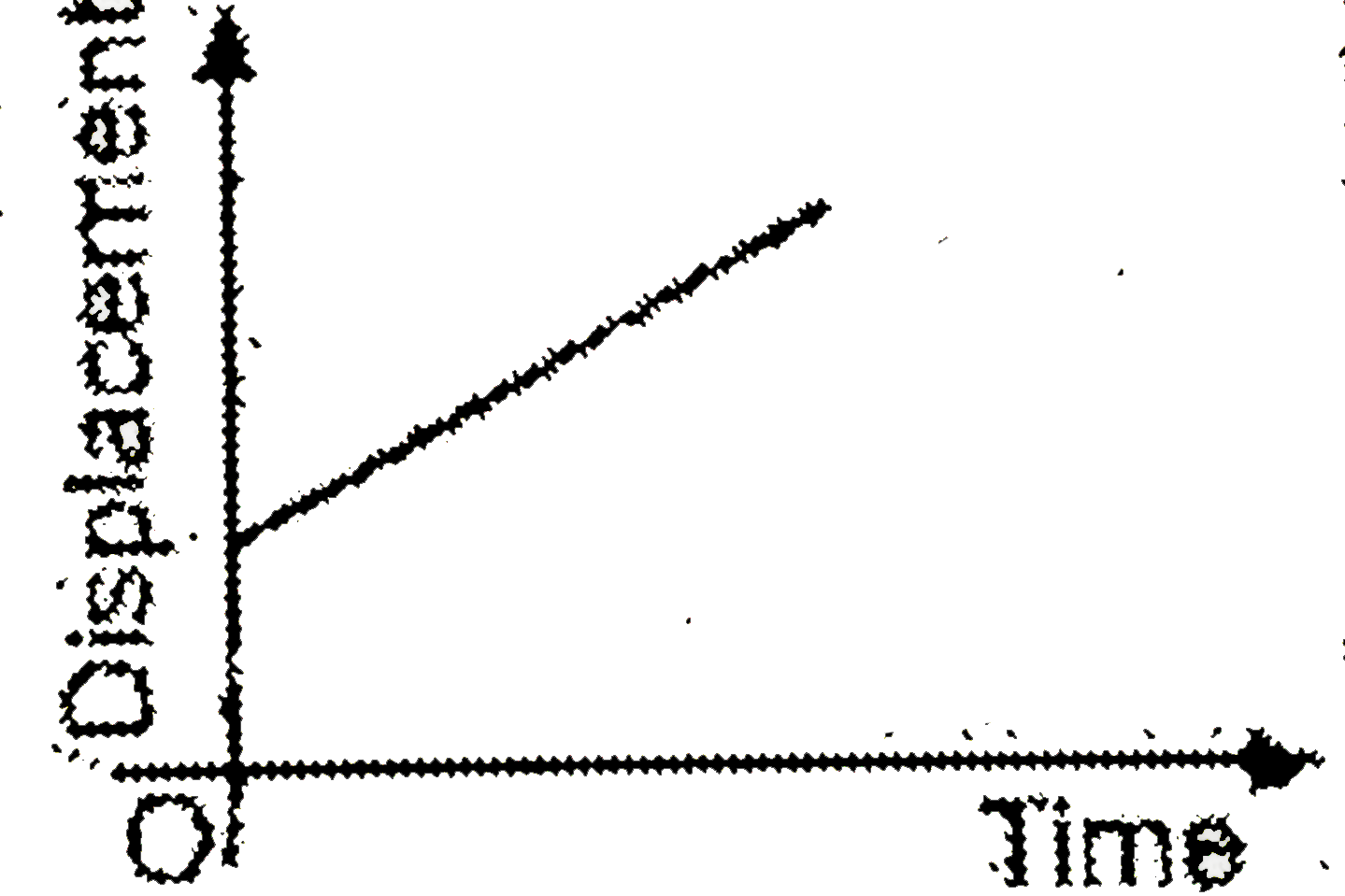 View Solution
View SolutionA particle performing SHM starts from mean position. The phase of that particle is π/s when it has
View SolutionA body is executing SHM. If the force acting on the body is 6N when the displacement is 2cm, then the force acting on the body at a displacement of 3cm is
View SolutionA partical executes SHM on a straigh line path. The amplitude of oscillation is 2cm. When the displacement of the particle from the mean position is 1cm, the magnitude of its acceleration is equal to that of its velocity. Find the time period of SHM, also the ms. velocity and ms. acceleration of SHM.
View SolutionThe positions of maximum displacement of a particle from the mean position of a transverse wave is called ______
View SolutionIn the previous problem, the displacement of the particle from the mean position corresponding to the instant mentioned is
View SolutionThe amplitude of a particle executing SHM is 4 cm. At the mean position, the speed of the particle is 16 cm/s. The distance of the particle from the mean position at which the speed of the particle becomes 8√3 cm/sec will be
View SolutionThe velocity of a particle in simple harmonic motion at displacement y from mean position is
View Solution


