A wheel is rotating with frequency of 500 rpm on a shaft, second identical wheel initially at rest is suddenly coupled on same shaft. The frequency of the resultant combination is
250 rps
500 rps
250 rpm
500rpm
The correct Answer is:C
To solve the problem, we need to determine the frequency of the resultant combination when a second identical wheel, initially at rest, is coupled to a rotating wheel.
1. Identify the initial conditions:
- The first wheel is rotating at a frequency of f1=500 rpm.
- The second identical wheel is initially at rest, so its frequency f2=0 rpm.
2. Understand the concept of coupling:
- When two identical wheels are coupled on the same shaft, they will share the same angular velocity after coupling.
- The total angular momentum of the system must be conserved.
3. Calculate the initial angular momentum:
- The angular momentum L of a rotating wheel can be expressed as L=Iω, where I is the moment of inertia and ω is the angular velocity.
- For the first wheel, the angular velocity ω1 can be calculated from its frequency:
ω1=2π×f160=2π×50060 rad/s
4. Calculate the moment of inertia:
- Since both wheels are identical, let the moment of inertia of one wheel be I.
- The total initial angular momentum of the system is:
Linitial=Iω1+Iω2=Iω1+0=Iω1
5. Determine the final angular momentum:
- After coupling, both wheels will rotate together at a new frequency ff. The angular velocity ωf will be:
ωf=2π×ff60
- The total moment of inertia after coupling is 2I (since there are two identical wheels).
- The final angular momentum is:
Lfinal=2Iωf
6. Apply conservation of angular momentum:
- According to the conservation of angular momentum:
Linitial=Lfinal
- Substituting the expressions we have:
Iω1=2Iωf
- We can cancel I from both sides (assuming I≠0):
ω1=2ωf
7. Solve for the final angular velocity:
- Rearranging gives:
ωf=ω12
8. Convert back to frequency:
- Since ωf=2π×ff60, we can substitute:
500×2π60=2(2π×ff60)
- Simplifying gives:
ff=5002=250 rpm
Final Answer:
The frequency of the resultant combination after coupling the two wheels is 250 rpm.
- The first wheel is rotating at a frequency of f1=500 rpm.
- The second identical wheel is initially at rest, so its frequency f2=0 rpm.
- When two identical wheels are coupled on the same shaft, they will share the same angular velocity after coupling.
- The total angular momentum of the system must be conserved.
- The angular momentum L of a rotating wheel can be expressed as L=Iω, where I is the moment of inertia and ω is the angular velocity.
- For the first wheel, the angular velocity ω1 can be calculated from its frequency:
ω1=2π×f160=2π×50060 rad/s
- Since both wheels are identical, let the moment of inertia of one wheel be I.
- The total initial angular momentum of the system is:
Linitial=Iω1+Iω2=Iω1+0=Iω1
- After coupling, both wheels will rotate together at a new frequency ff. The angular velocity ωf will be:
ωf=2π×ff60
- The total moment of inertia after coupling is 2I (since there are two identical wheels).
- The final angular momentum is:
Lfinal=2Iωf
- According to the conservation of angular momentum:
Linitial=Lfinal
- Substituting the expressions we have:
Iω1=2Iωf
- We can cancel I from both sides (assuming I≠0):
ω1=2ωf
- Rearranging gives:
ωf=ω12
- Since ωf=2π×ff60, we can substitute:
500×2π60=2(2π×ff60)
- Simplifying gives:
ff=5002=250 rpm
The frequency of the resultant combination after coupling the two wheels is 250 rpm.
Topper's Solved these Questions
Similar Questions
A wheel is rotasting ast an angular speed ω about its axis which is kept vertical. An identical wheel initially at rest is gently dropped into the sae axle and the two wheels start rotating with a common angular speed. Find this common angular speed.
View SolutionThe bob A of a pendulum released from a height h hits head-on another bob B of the same mass of an identical pendulum initially at rest. What is the result of this collision? Assume the collisio to be elastic (see figure).
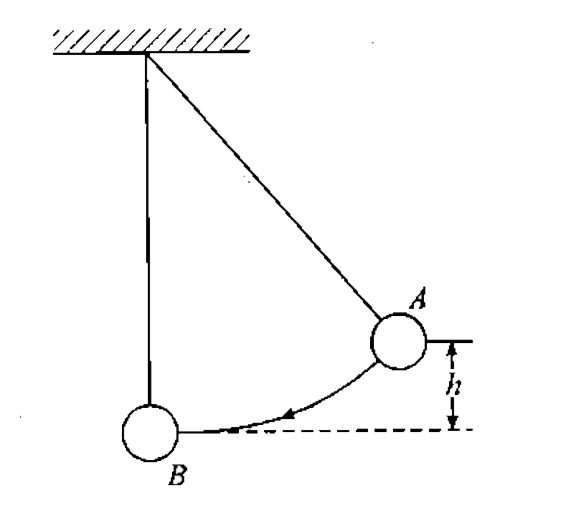
View Solution
Knowledge Check
wheel rotates with angular velocity 500 r.p.m. on a shaft. Second identical wheel axially at rest is suddenly coupled on same shaft. What is the total angular speed of the system? [Assume M.I. of shaft to be negligible]
A124 r.p.m.B500 r.p.m.C250 r.p.m.D750 r.p.m.A wheel is rotating freely at an angular speed of 800 rev/min on a shaft whose rotational inertia is negligible. A second wheel initially at rest with thrice the rotational inertia of the first is suddenly coupled to the same shaft. The fraction of original kinetic energy lost is
A23B13C14D12Two fly wheels A and B are mounted side by side with frictionless bearings on a common shaft. Their moments of inertia about the shaft are 5.0kgm2 and 20.0kgm2 respectively. Wheel A is made to rotate at 10 revolution per second. Wheel B, initially stationary, is now coupled to A with the help of a clutch. The rotation speed of the wheels will become
A2√5 rpsB0.5 rpsC2 rpsDNone of these
A wheel of moment of inertia 0.10kg−m2 is rotating about a shaft at an angular speed o 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with as common angular speed of 200 rev/minute. Find the moment of inertia o the second wheel.
View SolutionA wheel of a bicycle is rotating about its axis with an angular velocity of 100 rpm. When the brakes are applied, the wheel comes to rest in 10 s. Calculate the number of revolutions made by the wheel before coming to rest. Assume that the deceleration is constant.
View SolutionTwo fly wheels A and B are mounted side by side with frictionless bearings on a common shaft. Their moments of inertia about the shaft are 5.0 kg m2 and 20.0 kg m2 respectively. Wheel A is made to rotate at 10 revolution per second. Wheel B, initially stationary, is now coupled to A with the help of a clutch. The rotation speed of the wheels will become
View SolutionA fly wheel of moment of inertia I is rotating at n revolutions per sec. The work needed to double the frequency would be -
View SolutionA fly wheel of moment of inertia I is rotating at n revolutions per sec. The work needed to double the frequency would be -
View Solution
