Question

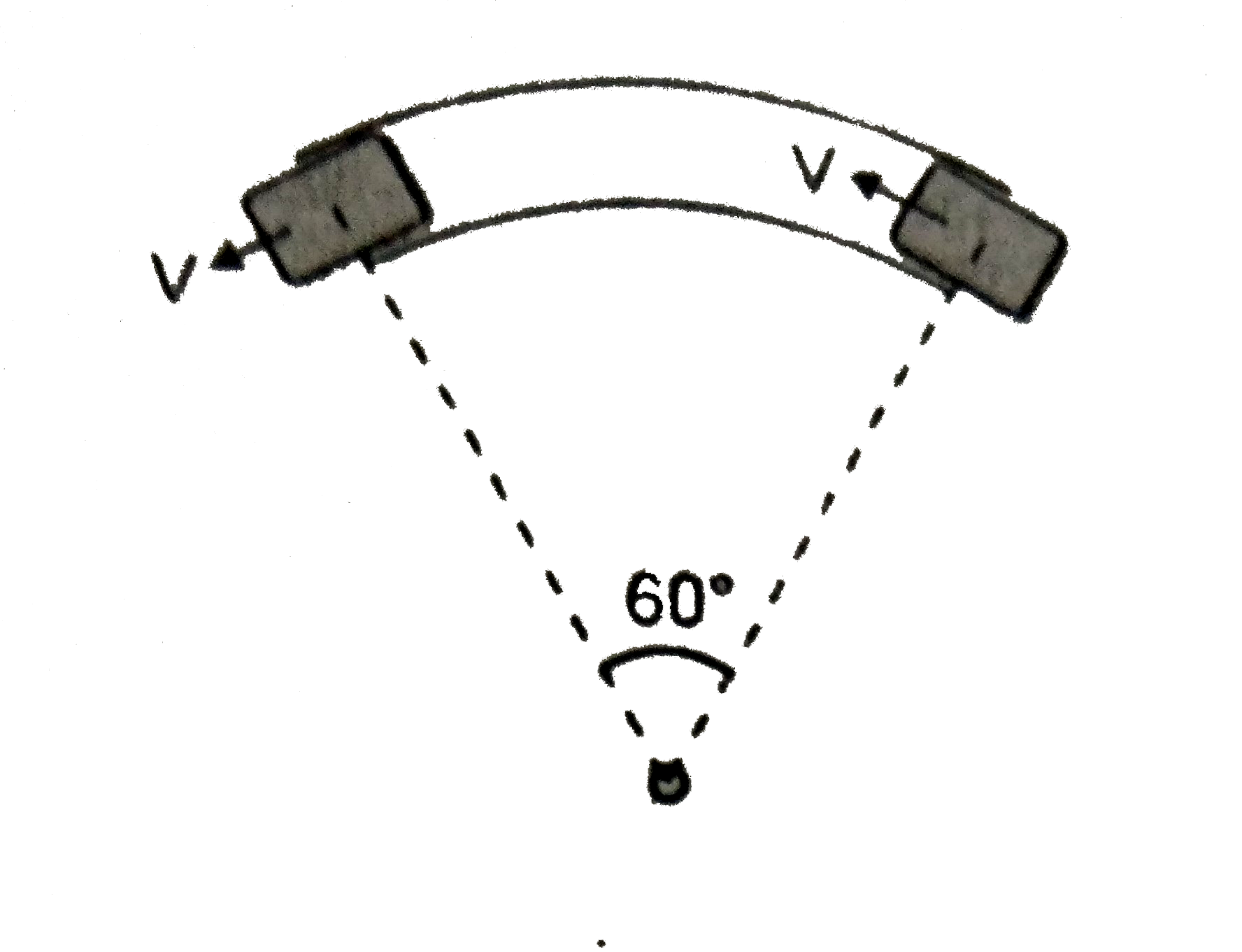
In the above question, the magnitude of the average acceleration over the arc of ${\displaystyle {60}^{\circ }}$ is

Options

A. `10 m//s^(2)`
B. `11 m//s^(2)`
C. `11.5 m//s^(2)`
D. `12 m//s^(2)`

Answer

C

Explanation

To solve the problem of finding the magnitude of the average acceleration over the arc of 60 degrees for an automobile moving around a curve, we can follow these steps:

1. Identify Given Values:
- Radius of the curve, \( R = 300 \) meters
- Constant speed of the automobile, \( V = 60 \) meters/second
- Angle of the arc, \( \theta = 60^\circ \)

2. Calculate Change in Velocity (\( \Delta V \)):
- The formula for change in velocity when moving along an arc is given by:
\( \Delta V = 2V \sin\left(\frac{\theta}{2}\right) \)
- Substitute the values:
\( \Delta V = 2 \times 60 \times \sin\left(\frac{60^\circ}{2}\right) = 2 \times 60 \times \sin(30^\circ) \)
- Since \( \sin(30^\circ) = \frac{1}{2} \):
\( \Delta V = 2 \times 60 \times \frac{1}{2} = 60 \text{ m/s} \)

3. Calculate Angular Velocity (\( \omega \)):
- The angular velocity can be calculated using the formula:
\( \omega = \frac{V}{R} \)
- Substitute the values:
\( \omega = \frac{60}{300} = \frac{1}{5} \text{ rad/s} \)

4. Calculate the Time Taken (\( T \)) to Cover the Arc:
- The time taken to cover the arc can be calculated using:
\( T = \frac{\theta}{\omega} \)
- Convert \( \theta \) from degrees to radians:
\( \theta = 60^\circ = \frac{\pi}{3} \text{ radians} \)
- Substitute the values:
\( T = \frac{\frac{\pi}{3}}{\frac{1}{5}} = \frac{5\pi}{3} \text{ seconds} \)

5. Calculate Average Acceleration (\( A_{avg} \)):
- The average acceleration can be calculated using the formula:
\( A_{avg} = \frac{\Delta V}{T} \)
- Substitute the values:
\( A_{avg} = \frac{60}{\frac{5\pi}{3}} = 60 \times \frac{3}{5\pi} = \frac{180}{5\pi} = \frac{36}{\pi} \text{ m/s}^2 \)
- Using \( \pi \approx 3.14 \):
\( A_{avg} \approx \frac{36}{3.14} \approx 11.46 \text{ m/s}^2 \)

6. Final Answer:
- The magnitude of the average acceleration over the arc of \( 60^\circ \) is approximately \( 11.46 \text{ m/s}^2 \).