A student is given a quiz with 10 true or false question, and he answers by sheer guessing. If X is the number of question answered correctly. If the student passes the quiz by getting 7 or maximum correct answer, then the probability that the student passes the quiz is
1132
1116
1164
11128
The correct Answer is:C
To solve the problem, we need to find the probability that a student passes a quiz by answering at least 7 out of 10 true or false questions correctly, given that he answers by sheer guessing.
1. Understanding the Problem:
The student answers 10 questions, each with two possible answers (True or False). The probability of answering a question correctly (P) is 1/2, and the probability of answering incorrectly (Q) is also 1/2.
2. Defining the Random Variable:
Let X be the number of questions answered correctly. X follows a binomial distribution with parameters n=10 (the number of questions) and p=1/2 (the probability of a correct answer).
3. Finding the Required Probability:
We need to find the probability that the student passes the quiz, which is defined as answering 7 or more questions correctly. Mathematically, this is expressed as:
P(X≥7)=P(X=7)+P(X=8)+P(X=9)+P(X=10)
4. Using the Binomial Probability Formula:
The probability mass function for a binomial distribution is given by:
P(X=k)=(nk)pk(1−p)n−k
For our case, n=10 and p=1/2. Therefore, the formula simplifies to:
P(X=k)=(10k)(12)10
5. Calculating Each Probability:
- For k=7:
P(X=7)=(107)(12)10=1201024
- For k=8:
P(X=8)=(108)(12)10=451024
- For k=9:
P(X=9)=(109)(12)10=101024
- For k=10:
P(X=10)=(1010)(12)10=11024
6. Summing the Probabilities:
Now we add these probabilities together:
P(X≥7)=P(X=7)+P(X=8)+P(X=9)+P(X=10)
P(X≥7)=1201024+451024+101024+11024=1761024
7. Simplifying the Result:
Simplifying 1761024:
176÷161024÷16=1164
Final Answer:
The probability that the student passes the quiz is 1164.
The student answers 10 questions, each with two possible answers (True or False). The probability of answering a question correctly (P) is 1/2, and the probability of answering incorrectly (Q) is also 1/2.
Let X be the number of questions answered correctly. X follows a binomial distribution with parameters n=10 (the number of questions) and p=1/2 (the probability of a correct answer).
We need to find the probability that the student passes the quiz, which is defined as answering 7 or more questions correctly. Mathematically, this is expressed as:
P(X≥7)=P(X=7)+P(X=8)+P(X=9)+P(X=10)
The probability mass function for a binomial distribution is given by:
P(X=k)=(nk)pk(1−p)n−k
For our case, n=10 and p=1/2. Therefore, the formula simplifies to:
P(X=k)=(10k)(12)10
- For k=7:
P(X=7)=(107)(12)10=1201024
- For k=8:
P(X=8)=(108)(12)10=451024
- For k=9:
P(X=9)=(109)(12)10=101024
- For k=10:
P(X=10)=(1010)(12)10=11024
Now we add these probabilities together:
P(X≥7)=P(X=7)+P(X=8)+P(X=9)+P(X=10)
P(X≥7)=1201024+451024+101024+11024=1761024
Simplifying 1761024:
176÷161024÷16=1164
The probability that the student passes the quiz is 1164.
Topper's Solved these Questions
Similar Questions
A student is given 6 questions in a true or false examination If he gets 4 or more correct answers he passes the examination.The probability that he passes the examination is
View SolutionIn answering a question on a multiple choice test for class XII, a student either knows the answer or guesses. Let 3/5 be the probability that he knows the answer and 2/5 be the probability that he guesses. Assume that a student who guesses at the answer will be correct with probability 1/3. Let E1,E2, E be the events that the student knows the answer, guesses the answer and answers correctly respectively.

Based on the above information, answer the following
What is the probability that the student knows the answer given that he answered it correctly?
View Solution
Knowledge Check
These is an objective type question with 4 answer choices exactly one of which is correct. A student has not studied the topic on which the question has been set. The probility that the student guesses the correct answer is
A1/2B1/4C1/8DNone of theseIn an entrance examinations there are multiple choice question. There are five possible answers to each question of which one is correct. The probability that a student knows the answer to a question is 80%. IF he gets the correct answer to the question, then the probability that he was guessing is
A19B110C121D120In a class of 10 student, probability of exactly I students passing an examination is directly proportional to i2. Then answer the following questions:
If a students selected at random is found to have passed the examination, then the probability that he was the only student who has passed the examination isA1/3025B1/605C1/275D1/121
Each of the total fice questions in amultiple choice examination has four choices, only one of which is correct.A student is attempting to guess the amswer . The renadom varible X is the number of question answerred correctly. What is the probability that the student will giveat least one correct answer ?
View SolutionIn answering a question on a multiple choice test a student either knows the answer or guesses. Let the probability that he knows the answer is 34 and probability that he guesses is 14. Assuming that a student who guesses the answer and given correct answer is 14. What is the probability that student knows the answer given that he answered it correctly?
View SolutionRead the bar graph given below and answer the following questions:
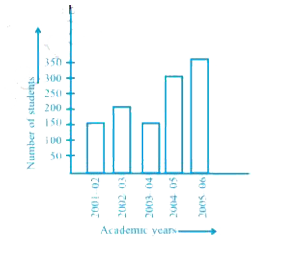
In which year is the number of students maximum?
View SolutionIn an examination, there are 3 multiple choice questions and each question has 4 choices. If a student randomly selects answer for all the 3 questions, what is the probability that the student will not answer all the 3 questions correctly ?
View SolutionIn an examination, there are 3 multiple-choice questions and each question has 4 choices. If a student randomly select an answer for all the three question, what is the probability that the students will not answer all the three questions correctly?
View Solution