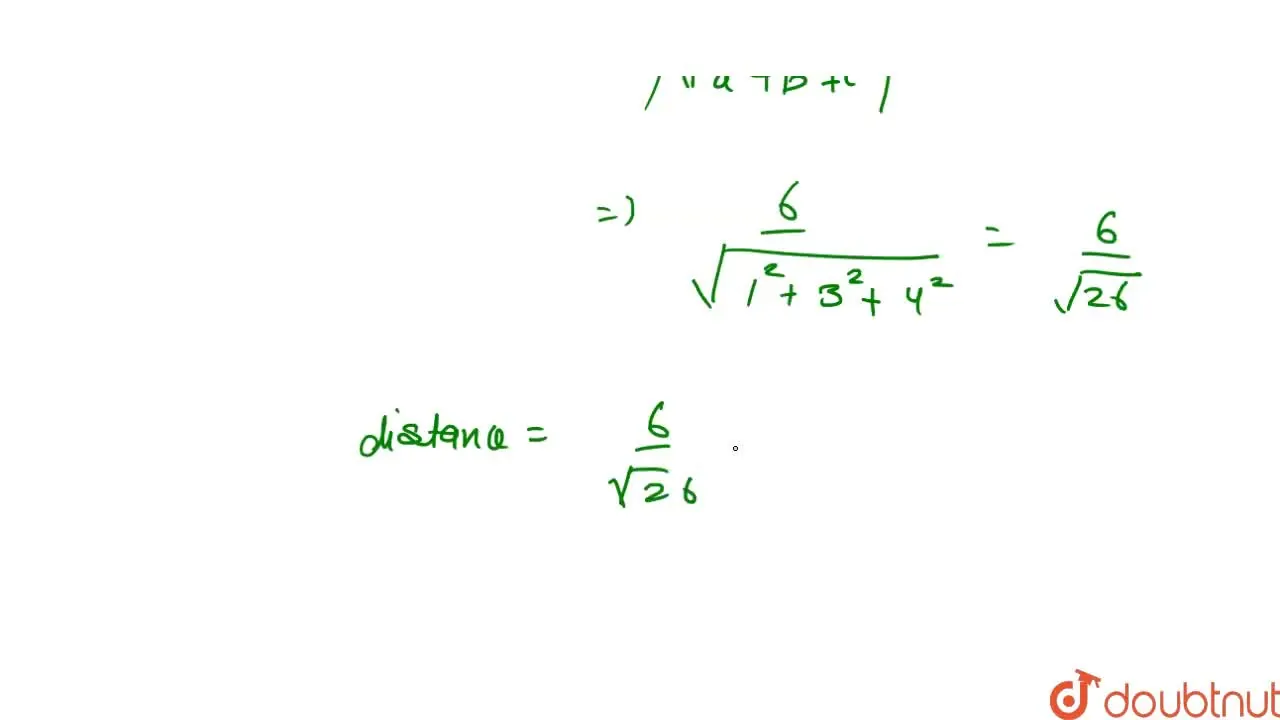The length of the perpendicular from origin to the plane x−3y+4z=6 is
3√26
6√26
3√13
6√13
The correct Answer is:B
Step by step video, text & image solution for The length of the perpendicular from origin to the plane x-3y+4z=6 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Related Playlists
Similar Questions
The length of the perpendicular from the origin to the plane 3x+4y+12z=52 is
View SolutionIf a plane cuts intercepts -6,3,4 on the co-ordinate axes, then the length of the perpendicular form the origin to the plane is
View SolutionFind the length of the perpendicular drawn from the origin to the plane 2x 3y+6z+21=0.
View SolutionFind the length of the perpendicular from the origin to the line 4x+3y-2=0
View SolutionA plane cuts off intercepts 3,−4,6 on the coordinate axes. The length of perpendicular from the origin to this plane is
View SolutionFoot of the perpendicular drawn from the origin to the plane 2x−3y+4z=29 is
View SolutionThe foot of the perpendicular drow from origin to the plane x+y+3z−4=0 is
View SolutionFind the direction cosines of the normal to the plane 4x−3y+5z=25 and the length of the perpendicular from the origin on this plane
View SolutionFoot of perpendicular drawn from the origin to the plane 2x−3y+4z=29 is
View SolutionThe coordinates of the foot of the perpendicular drawn from the origin to the plane 2x−3y+4z−6=0 is
View Solution