At what frequency 1 Henry inductance offers the same impedance as 1μF capacitor?
5002πHz
500πHz
500πHz
1000πHz
The correct Answer is:B
To solve the problem of finding the frequency at which a 1 Henry inductance offers the same impedance as a 1 microfarad capacitor, we can follow these steps:
1. Identify Given Values:
- Inductance L=1H
- Capacitance C=1μF=1×10−6F
2. Understand Impedance Relationships:
- The impedance of an inductor ZL is given by:
ZL=jωL
- The impedance of a capacitor ZC is given by:
ZC=1jωC
- For the inductance and capacitance to have the same impedance in magnitude, we set:
|ZL|=|ZC|
- This leads to:
ωL=1ωC
3. Rearranging the Equation:
- Multiplying both sides by ω:
ω2LC=1
- This can be rearranged to find ω:
ω2=1LC
- Therefore,
ω=1√LC
4. Substituting Values:
- Substitute L=1H and C=1×10−6F:
ω=1√1×1×10−6=1√10−6=103rad/s
5. Convert Angular Frequency to Frequency:
- The relationship between angular frequency ω and frequency f is:
ω=2πf
- Therefore,
f=ω2π=1032π
- Simplifying this gives:
f=10002×3.14=10006.28≈159.15Hz
6. Final Calculation:
- To express it in terms of 500π:
f≈500πHz
Conclusion:
The frequency at which a 1 Henry inductance offers the same impedance as a 1 microfarad capacitor is:
f≈500πHz
- Inductance L=1H
- Capacitance C=1μF=1×10−6F
- The impedance of an inductor ZL is given by:
ZL=jωL
- The impedance of a capacitor ZC is given by:
ZC=1jωC
- For the inductance and capacitance to have the same impedance in magnitude, we set:
|ZL|=|ZC|
- This leads to:
ωL=1ωC
- Multiplying both sides by ω:
ω2LC=1
- This can be rearranged to find ω:
ω2=1LC
- Therefore,
ω=1√LC
- Substitute L=1H and C=1×10−6F:
ω=1√1×1×10−6=1√10−6=103rad/s
- The relationship between angular frequency ω and frequency f is:
ω=2πf
- Therefore,
f=ω2π=1032π
- Simplifying this gives:
f=10002×3.14=10006.28≈159.15Hz
- To express it in terms of 500π:
f≈500πHz
The frequency at which a 1 Henry inductance offers the same impedance as a 1 microfarad capacitor is:
f≈500πHz
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS Book:MARVEL PUBLICATIONChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS Exercise:TEST YOUR GRASP - 16
Explore 30 Videos
- ELASTICITYBook:MARVEL PUBLICATIONChapter:ELASTICITYExercise:Test Your Grasp - 5
Explore 15 Videos
- ELECTRONS AND PHOTONS Book:MARVEL PUBLICATIONChapter:ELECTRONS AND PHOTONS Exercise:TEST YOUR GRASP - 17
Explore 15 Videos
Similar Questions
(a) At what frequency would a 12 mH inductor and a 10 μF capacitor have the same reactance? (b) What would the reactance be? (c) Show that this frequency would be the natural frequency of an oscillating circuit with the same L and C.
View SolutionFind the natural frequency of a circuit jcontaininig inductance of 100μH and a capacity of 0.1μF. To which wavelength will its respone be maximum? How long will the oscillations last ?
View Solution
Knowledge Check
For high frequency, a capacitor offers
AMore reactanceBLess reactanceCZero reactanceDInfinite reactanceIn resonating circuit value of inductance and capacitance is 0.1H and 200μF. For same resonating frequency if value of inductance is 100H then necessary value of capacitance in μF will be -
A4B0.2C2D0.3The frequency at which the inductive reactance of 2H inductance will be equal to the capactive reactance of 2μF capactiance (nearly)
A80HzB40HzC60HzD20Hz
A coil has an inductance of 1 henry. (a) At what frequency will it have a reactance of 3142 ohm? (b) What should be the capacity of a condenser which has the same reactanc at frequency ?
View SolutionThe figure shows the graphical variation of the rectance of a capacitor with frequency of acsource.
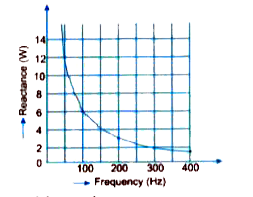
(a) Find the capacitance of the capacitor.
(b) An ideal inductor has the same reactance at 100 Hz frequency as the capacitor has at the same frequency. Find the value of inductance of the inductor.
(c ) Draw the graph showing the variation of the rectance of this inductor with frequency.
View SolutionDefine mutual inductance of 1 Henry.
View SolutionIf frequency of R- L circuit is f then impedence will be
View SolutionAn alternating current of 1.5 mA with angular frequency 100 rad/s flows through a 10kΩ resistor and a 0.50μF capacitor in series. The rms potential drop across the capacitor is
View Solution

