D.E. of all circules of a given radius a and variable centre (h, k) is
(1+y21)3+a2(y2)2=0
(1+y21)2+a2(y2)3=0
(1+y21)3=a2(y2)2
2xdx+2ydt=a2
The correct Answer is:C
Step by step video, text & image solution for D.E. of all circules of a given radius a and variable centre (h, k) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIAL EQUATIONSBOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - MULTIPLE CHOICE QUESTIONS (PREVIOUS YEARS MHT - CET EXAM QUESTIONS)
13 Videos
- DIFFERENTIAL EQUATIONSBOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - TEST YOUR GRASP
14 Videos
- CONTINUITY F FUNCTIONSBOOK - MARVEL PUBLICATIONCHAPTER - CONTINUITY F FUNCTIONSEXERCISE - MULTIPLE CHOICE QUESTIONS
131 Videos
- DIFFERENTIATIONBOOK - MARVEL PUBLICATIONCHAPTER - DIFFERENTIATIONEXERCISE - MULTIPLE CHOICE QUESTIONS (TEST YOUR GRASP - II : CHAPTER 11)
24 Videos
Similar Questions
The differential equation dydx=√1−y2y determines a family of circle with (a) variable radii and a fixed centre at(0,1) (b) variable radii and a fixed centre at (0,−1)(c) Fixed radius 1 and variable centres along the x-axis. (d) Fixed radius 1 and variable centres along the y-axis.
View SolutionOrder of the differential equation of the family of all concentric circles centred at (h,k) is
View Solution
Knowledge Check
The differential equation of all circles whose radius is 5 centre is any point (h,k) is
A25(d2ydx2)+(1+(dydx)2)2=0B25(d2ydx2)−(1+(dydx)2)2=0C25(d2ydx2)+(1+(dydx)2)3=0D25(d2ydx2)−(1+(dydx)2)3=0The kinetic energy of partical moving along a circule of radius R depends upon the distance covered S and given by K=aS where a is a constant. The the force acting on the partical is
AaSRB2aS2RCaS2R2D2aSRThe differential equation for all circles with centre (h,0) and radius r,h and r being arbitary constants is
Ay2−2xydydx−x2=0By2−2xydydx+x2=0Cy2+2xydydx−x2=0Dy2+2xydydx+x2=0
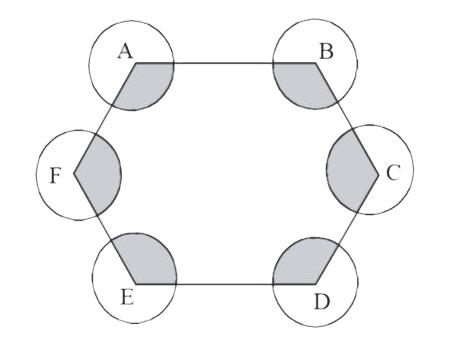
ABCDEF is a regular hexagon. With vertices A, B, C, D, E and F as the centres, circles of same radius ‘r’ are drawn. Find the area of the shaded portion shown in the given figure.
View SolutionDraw any circle and mark(a) its centre (b) a radius(c) a diameter (d) a sector(e) a segment (f) a point in its interior(g) a point in its exterior (h) an arc
View SolutionMagnetic field intensity H at the centre of a circular loop of radius r carrying current I e.m.u. is
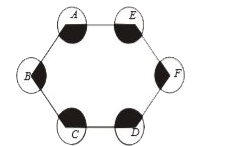
View SolutionFind the sum of the areas of the shaded sectors given that ABCDEF is any hexagon and all the circles are of same radius r with different vertices of the hexagon as their centres as shown in the figure.
View SolutionThe order of differential equation of all circles of given radius 'a' is
View Solution
