L-C-R परिपथ को समझाइये एवं परिपथ की परिणामी प्रतिबाधा तथा धारा का आयाम ज्ञात कीजिए ।
चित्र (a) के अनुसार, माना कि L प्रेरकत्व की एक कुण्डली C धारिता का एक संधारित्र तथा R प्रतिरोध के एक चालक को प्रत्यावर्ती स्त्रोत के साथ श्रेणीक्रम में जोड़ा गया है स्त्रोत का वोल्टेज समीकरण निम्नलिखित है -
V=V0sinωt . . .(1)
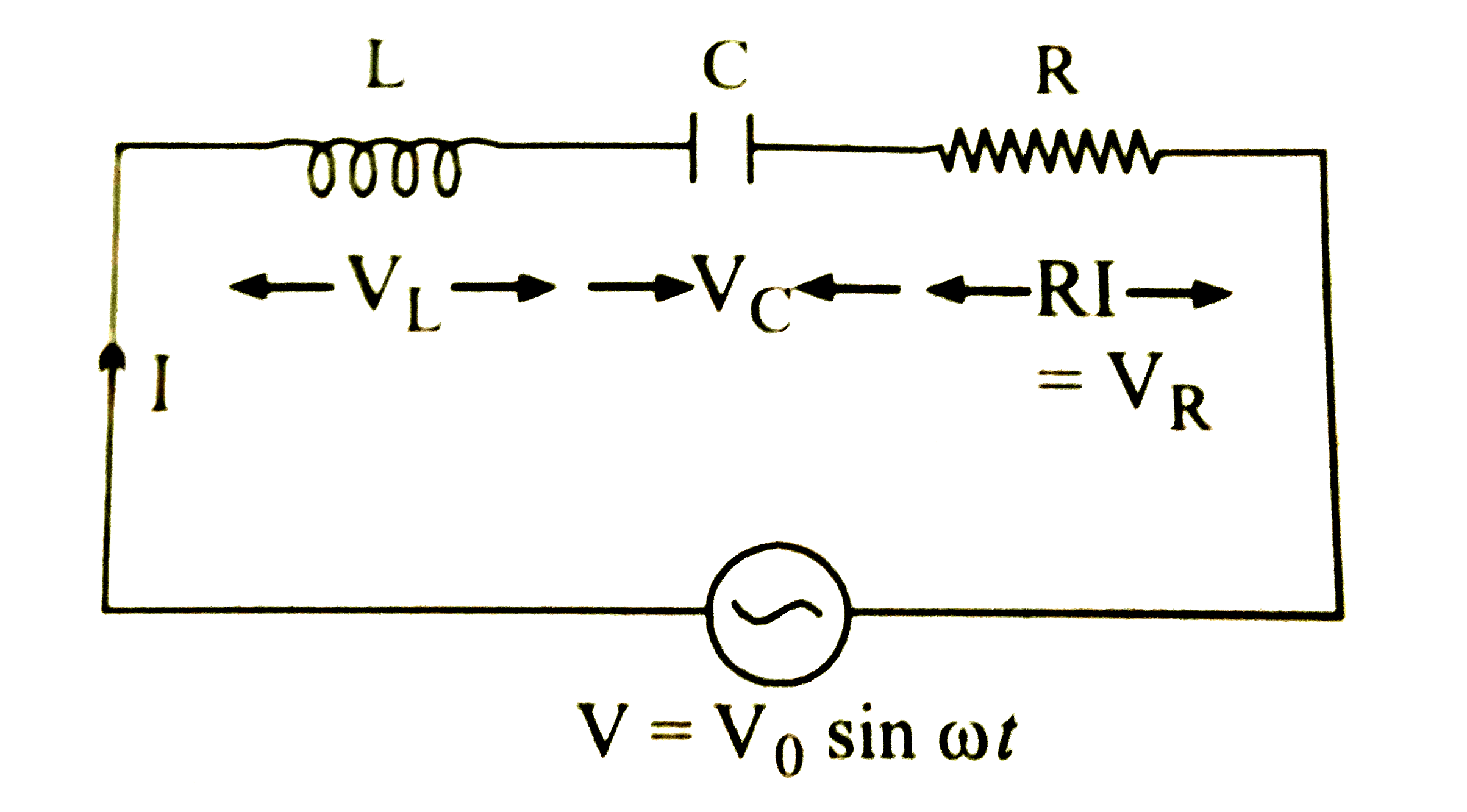
यदि किसी क्षण परिपथ में प्रवाहित धारा I हो, तो प्रेरकत्व L के सिरों का विभवान्तर VL=IXL, धारिता C के सिरों का विभवान्तर VC=IXC, तथा प्रतिरोध R के सिरों का विभवान्तर VR=IR होगा | विभवान्तर VR तथा I सामान कला में होते है विभवान्तर VL, धारा I से 90∘ अग्रगामी एवं विभवान्तर VC धारा I से 90∘ पश्चगामी होता है
अर्थात VL और VC के बीच 180∘ का कलान्तर होगा ।
अतः इस परिपथ का फेजर आरेख चित्र (b) के अनुसार होता है जिससे यह स्पष्ट है कि VL और VC का परिणामी VL−VC होगा । अब यदि परिपथ का परिणामी वोल्टेज V हो , तो
V2=V2R+(VL−VC)2
=I2R2+(IXL−IXC)2
=I2[R2+(XL−XC)2]
∴(परिणामी विभवान्तर)2=V2=I2[R2+(ωL−1ωC)2]
∴V2I2=R2+(ωL−1ωC)2
या VI=√R2+(ωL−1ωC)2 . . . . (2)
ओम के नियमानुसार VI परिपथ का प्रभावी प्रतिरोध अर्थात प्रतिबाधा Z होती है अतः L-C-R परिपथ की प्रतिबाधा
Z=VI=√R2+(ωL−1ωC)2 . . . . (3)
यही L-C-R परिपथ की प्रतिबाधा का सूत्र है चित्र (b) से स्पष्ट है कि यदि आरोपित प्रत्यावर्ती वोल्टेज V तथा प्रवाहित प्रत्यावर्ती धारा के बीच कलान्तर ϕ हो, तो समकोण त्रिभुज OAB से,
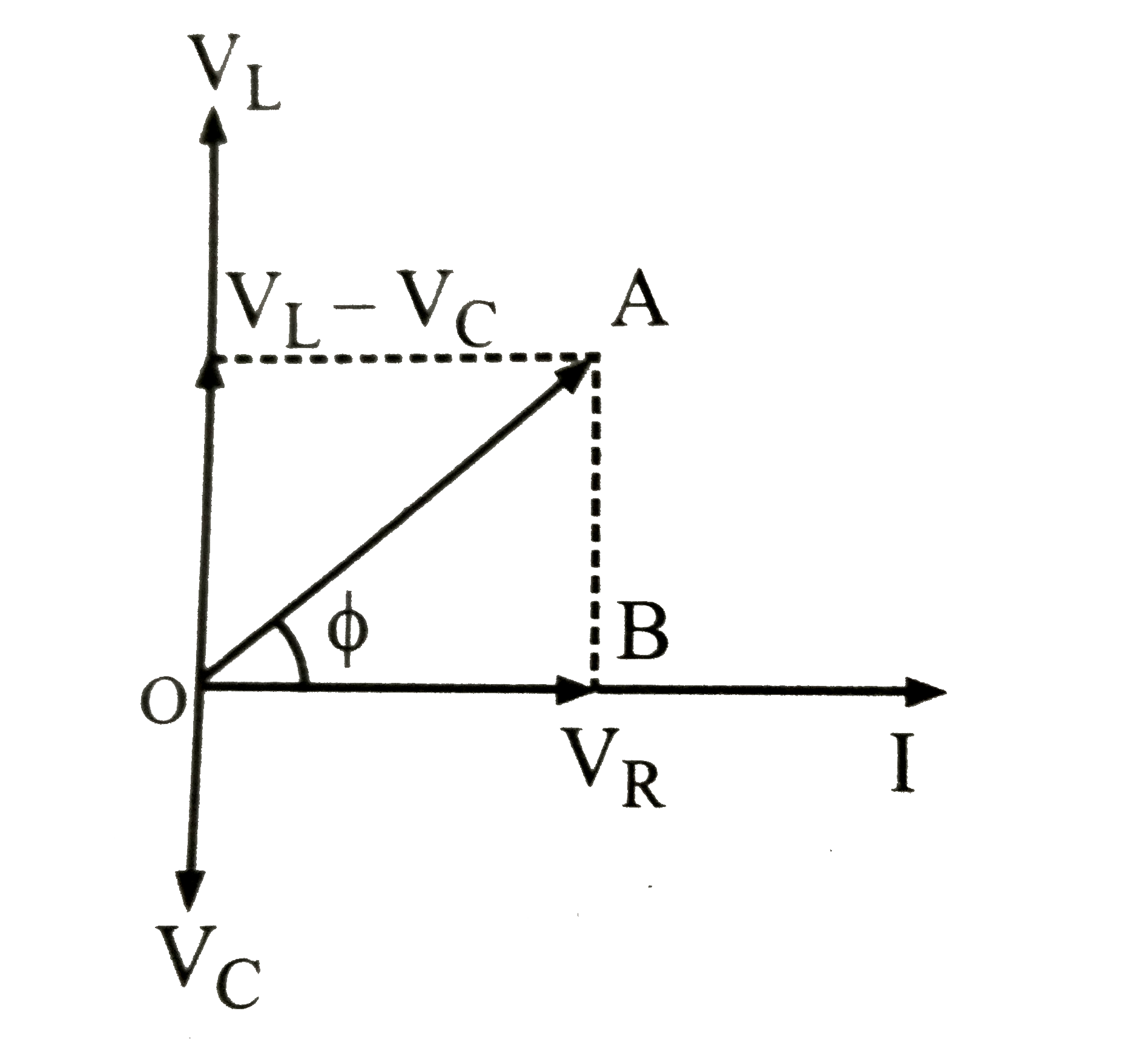
tanϕ=ABOB=VL−VCVR
=IXL−IXCIR=XL−XCR
=ωL−1ωCR
∴ ϕ=tan−1⎛⎝ωL−1ωCR⎞⎠ . . .(4)
यही प्रत्यावर्ती L-C-R परिपथ में धारा तथा वोल्टेज के बीच कलान्तर का सूत्र है अतः परिपथ में प्रवाहित प्रत्यावर्ती धारा का समीकरण अग्रलिखित होगा -
I=I0sin(ωt+ϕ)
=V0√R2+(ωL−1ωC)2
sin⎡⎢
⎢⎣ωt−tan−1(ωL−1ωC)R⎤⎥
⎥⎦ . . .(5)
यही L-C-R परिपथ में प्रवाहित प्रत्यावर्ती धारा का समीकरण है जिससे यह स्पष्ट होता है कि धारा की वोल्टेज से अग्रता अथवा पश्चता L तथा C के मान पर निर्भर करता है
समी. (5) से स्पष्ट है यदि
ωL=1ωC . . . (6)
तथा समी. (5) से स्पष्ट है कि tanϕ=0, अर्थात धारा तथा वोल्टेज सामान कला में होंगे तथा प्रतिबाधा का मान न्यूनतम होने के कारण धारा अधिकतम होगी । इस स्थिति को अनुनादी स्थिति कहते है
पुनः समी. (6) से,
ω2=1LC या ω=1√LC
या 2πf=1√LC
f=12π√LC
यही अनुनादी आवृत्ति का व्यंजक है ।
Topper's Solved these Questions
- प्रत्यावर्ती धारा BOOK - PRABODH PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - दीर्घ उत्तरीय प्रश्न
1 Videos
- प्रत्यावर्ती धारा BOOK - PRABODH PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - आंकिक प्रश्न
15 Videos
- प्रत्यावर्ती धारा BOOK - PRABODH PUBLICATIONCHAPTER - प्रत्यावर्ती धारा EXERCISE - आंकिक प्रश्न
15 Videos
- परमाणु BOOK - PRABODH PUBLICATIONCHAPTER - परमाणु EXERCISE - मूल्य आधारित प्रश्न
1 Videos
- प्रत्यावर्त्ती धाराBOOK - PRABODH PUBLICATIONCHAPTER - प्रत्यावर्त्ती धाराEXERCISE - मूल्य आधारित प्रश्न
8 Videos
Similar Questions
निम्नांकित बिन्दुओ के आधार पर ट्रांसफॉर्मर का वर्णन कीजिए -
(i) सिद्धांत, (ii) प्रकार एवं नामांकित रेखाचित्र, (iii) परिणमन अनुपात का सूत्र, (iv) ट्रांसफॉर्मर में परिणमन अनुपात का सूत्र ट्रांसफॉर्मर में ऊर्जा क्षय ।
View Solutionएक 100Ω का प्रतिरोधक 200 V, 50 Hz आवृत्ति से संयोजित है
(a) परिपथ में धारा का मान कितना है ?
(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय होती है |
View Solutionएक 100Ω का प्रतिरोधक 200 V, 50 Hz आवृत्ति से संयोजित है
(a) परिपथ में धारा का मान कितना है ?
(b) एक पूरे चक्र में कितनी नेट शक्ति व्यय होती है |
View Solutionहाइड्रोजन परमाणु के बोर सिद्धांत के अनुसार स्थायी कक्षा में इलेक्ट्रॉन की कुल ऊर्जा E =−13⋅6n2eV हैं , जहाँ n कक्षा की संख्या हैं । इलेक्ट्रॉन की कुल ऊर्जा ऋणात्मक हैं अर्थात् इलेक्ट्रॉन नाभिक से बद्ध होता हैं । जैसे - जैसे n का मान बढ़ता है ऊर्जा का ऋणात्मक मान घटता हैं अर्थात् बाह्रा कक्षा में ऊर्जा बढ़ते क्रम में होती हैं । उपरोक्त अनुच्छेद को पढ़कर निम्न प्रश्नों का उत्तर दीजिए - (i) H - परमाणु की मूल ऊर्जा अवस्था की ऊर्जा क्या होती हैं तथा यह क्या दर्शाती हैं ?
(ii) जब इलेक्ट्रॉन किसी उत्तेजित ऊर्जा अवस्था में होता हैं तो उससे इलेक्ट्रॉन को अलग करना आसान होता हैं , क्यों ?
(iii) यह हमारे जीवन में किस प्रकार उपयोगी हो सकता हैं ?
View Solutionट्रांसफॉर्मर एक ऐसा विद्युत यंत्र है जिमसे a.c विभव में परिवर्तन किया जाता है। यह अन्योन्य प्रेरकत्व के सिद्धान्त पर कार्य करता है अर्थात जब कुण्डली से सम्बद्ध चुम्बकीय फ्लक्स के मान में परिवर्तन होता है। इसके निकट की कुण्डली में एक वि वा बल प्रेरित होता है। एक आदर्श ट्रांसफॉर्मर के लिए
EsEp=IpIs=msmp
जहाँ संकेतो के सामान्य अर्थ है। उपरोक्त अनुच्छेद को पढ़कर निम्न प्रश्नो के उत्तर दीजिए।
एक ट्रांसफॉर्मर के प्राथमिक कुण्डली में 20 एवं द्वितीयक कुण्डली में 200 फेरे है। यदि प्राथमिक कुण्डली को 220 वोल्ट d.c स्त्रोत से जोड़े तब द्वितीयक कुण्डली के सिरों पर किनता वोल्ट होगा ?
View Solution283 v शिखर वोल्टता एवं 50HZ आवृति की एक ज्यावक्रीय वोल्टता एक श्रेणी बद्ध LCR परिपथ से जुडी है जिसमे R= 3Ω, L= 25.48mH एवं C= 796microfared है| ज्ञात कीजिये (a) परिपथ की प्रतिबाधा (b) स्रोत के सिरों के बीच लगी वोल्टता एवं परिपथ में प्रवाहित होने वाली धारा के बीच कालान्तर (c) परिपथ में होने वाला शक्ति क्षय (d) शक्ति गुणांक
माना कि पूर्व उदाहरण में वर्णित स्रोत की आवर्ती परिवर्तनशील है|(a) स्रोत कि किसी आवृति पर अनुनाद होगा| (b) अनुनाद की अवस्था में प्रतिबाधा, का धारा एवं क्षयित शक्ति की गणना कीजिए|
View Solutionसही युग्म बनाइए-
(i)प्रेरणिक प्रतिघात(a)√R2+X2L(ii)धारितिया प्रतिघात(b)√R2+(XL−XC)2(iii)R-Lपरिपथ की प्रतिबाधा(c)12πfC(iv)R−Cपरिपथ की प्रतिबाधा(d)ωL(v)LCR परिपथ की प्रतिबाधा(e)√R2+X2C
View Solutionविद्युत धारा और परिपथ | विद्युत परिपथ आरेख
View Solutionविद्युत धारा और परिपथ | विद्युत परिपथ आरेख | विद्युत विभव तथा विभवान्तर
View SolutionLc- परिपथ || अनुनादी परिपथ || श्रेणी तथा समान्तर अनुनादी परिपथ
View Solutionशुद्ध R - परिपथ || शुद्ध L - परिपथ || शुद्ध C - परिपथ
View SolutionL-परिपथ, L-R परिपथ ,LC - परिपथ
View SolutionR-L, R-L-C परिपथ
View Solutionविद्युत धारा और परिपथ#!#विद्युत परिपथ आरेख
View Solutionप्रत्यावर्ती धारा और दिश्ट धारा मे अंतर #!#प्रत्यावर्ती धारा परिपथ मे वोल्टता तथा धारा के बीच कलांतर#!#प्रतिरोध,प्रतिघात और प्रतिबाधा मे अंतर #!#प्रत्यावर्ती धारा परिपथ
View Solutionप्रत्यावर्ती धारा परिपथ जिसमे ओमीय प्रतिरोध हो#!#प्रत्यावर्ती धारा परिपथ जिसमे संधारित्र हो#!#प्रत्यावर्ती धारा परिपथ जिसमे प्रेरकत्व हो
View Solution
