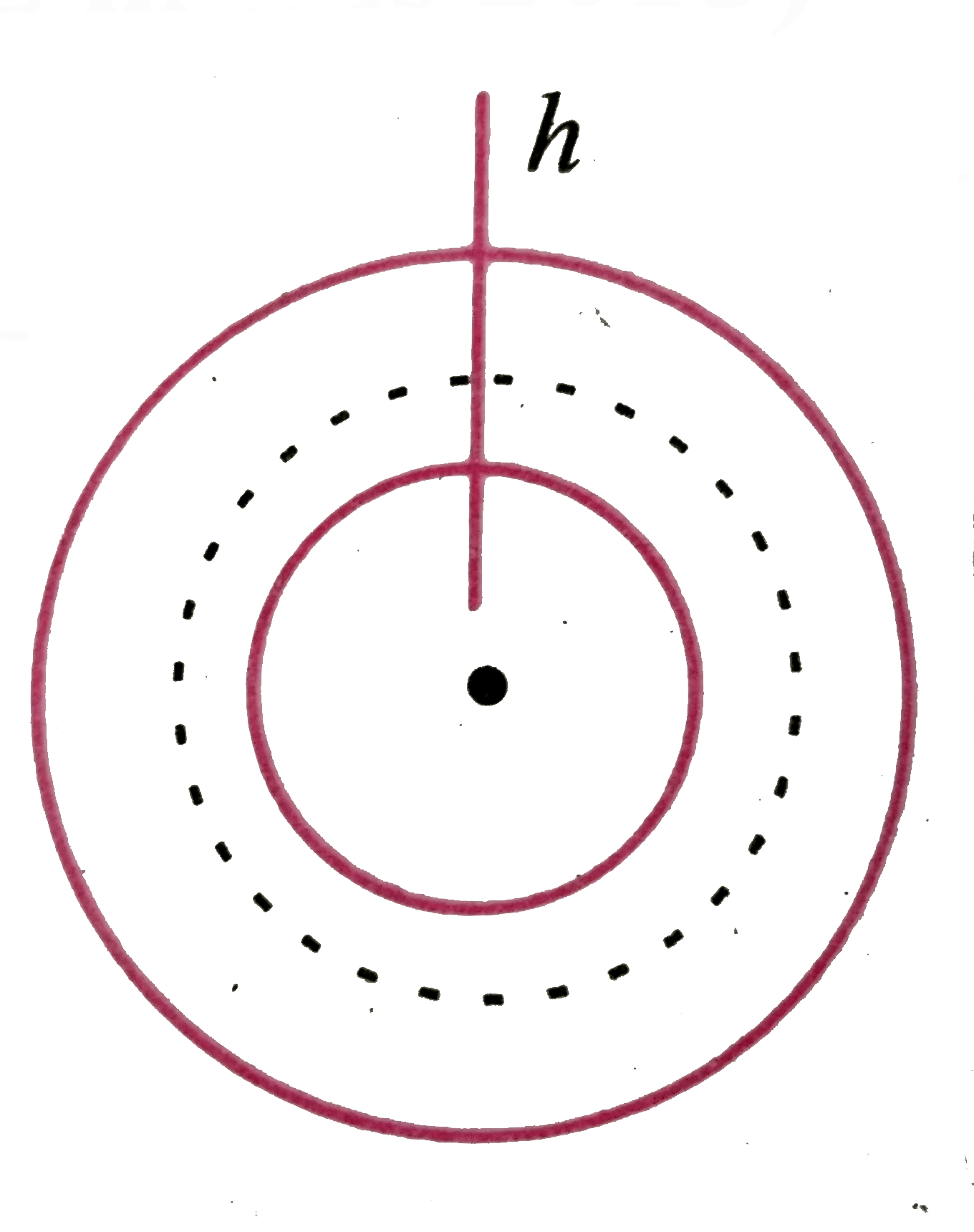
एक पतली $b = 2 a$ की चकती में a त्रिज्या का सकेंद्री छिद्र किया गया। एकसमान आवेश घनत्व $σ$ है। केंद्र से h ऊंचाई पर विद्युत क्षेत्र $(h < < a)$ का मान होगा -

A

$\frac{σ h}{2 a ε_{0}}$

B

$\frac{σ h}{4 a ε_{0}}$

C

$\frac{σ h}{8 a ε_{0}}$

D

$\frac{σ h}{a ε_{0}}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:a

आवेशित चालक से x दुरी पर अक्षीय स्थिति से,
विद्युत - क्षेत्र $E = \frac{σ}{2 ε_{0}} [1 - \frac{1}{\sqrt{R^{2} + x^{2}}}]$
पूर्ण चकती R = 2a के कारण h ऊँचाई पर विद्युत - क्षेत्र
$E_{1} = \frac{σ}{2 ε_{0}} [1 - \frac{h}{\sqrt{4 a^{2} + h^{2}}}]$
$= \frac{σ}{2 ε_{0}} [1 - \frac{h}{2 a}], [h < < a]$
h ऊँचाई R = a पर चकती के कारण विद्युत-क्षेत्र
$E_{2} = \frac{σ}{2 ε_{0}} [1 - \frac{h}{2 a}]$
अतः सम्पूर्ण चकती के कारण विद्युत - क्षेत्र
$E = E_{1} - E_{2} = \frac{σ h}{4 ε_{0} a}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

PRABODH PUBLICATION-विद्युत आवेश एवं क्षेत्र -बहुविकल्पीय प्रश्न : प्रतियोगी परीक्षा हेतु

Home
Ask Doubt
Profile