संलग्न चित्र में, त्रिभुज ABC शीर्ष बिन्दु A पर एक समकोण त्रिभुज है | जहाँ AB = 6 सेमी., BC = 10 सेमी. तथा $I, Δ A B C$ के अन्त:वृत्त का केन्द्र है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए |

Video Solution

Text Solution

Verified by Experts

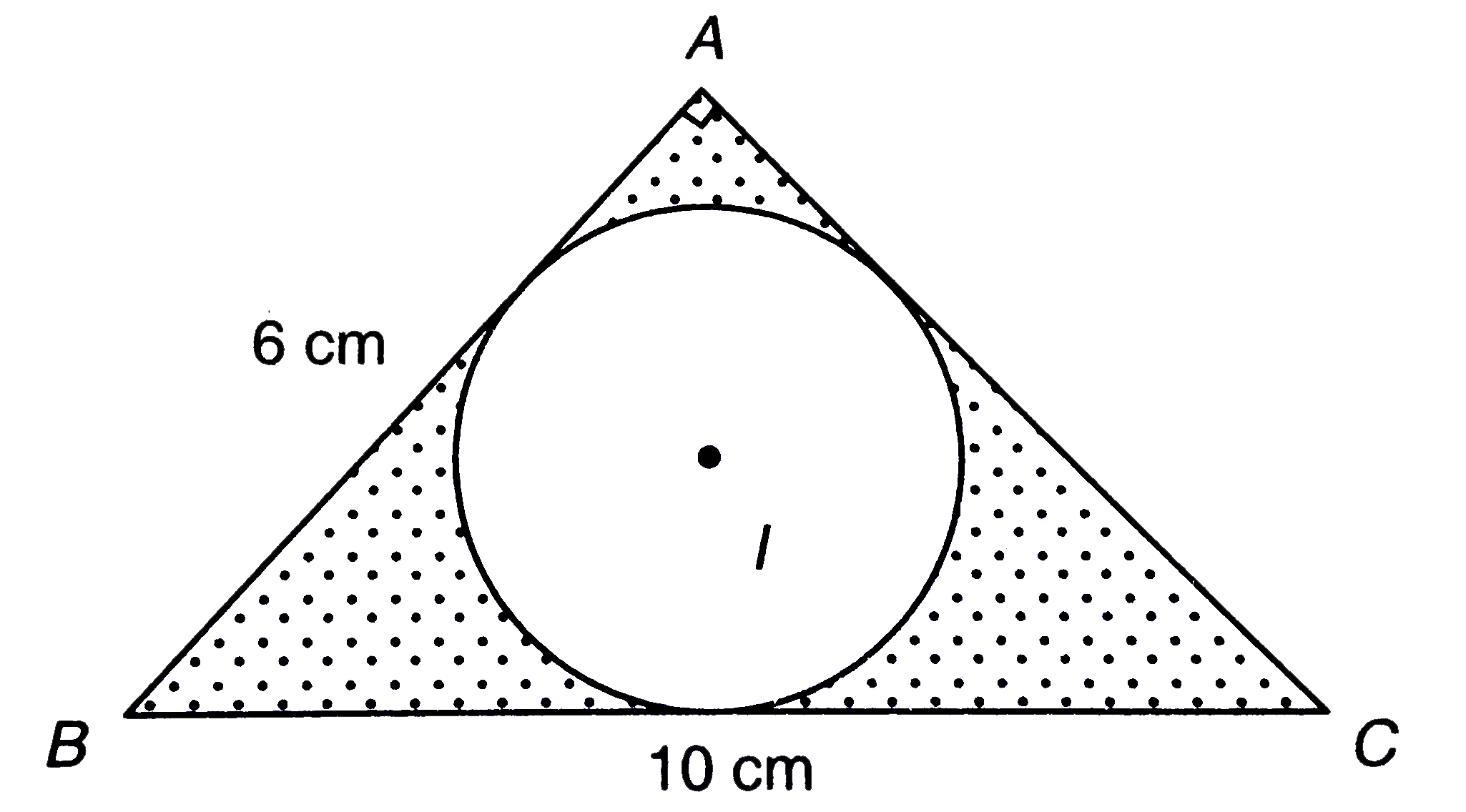
$Δ A B C$ में, पाइथागोरस प्रमेय का प्रयोग करने पर,
$B C^{2} = A B^{2} + A C^{2}$
$\Rightarrow A C^{2} = B C^{2} - A B^{2}$
$\Rightarrow A C^{2} = 100 - 36 = 64$
$\Rightarrow A C = 8 सेमी.$
$∴ Δ A B C का क्षेत्रफल = \frac{1}{2} \times A B \times A C$
$\Rightarrow Δ A B C का क्षेत्रफल = \frac{1}{2} \times 6 \times 8 {सेमी.}^{2} = 24 {सेमी.}^{2}$
माना अन्त:वृत्त की त्रिज्या r सेमी. है |
स्पष्ट है की,
$Δ A B C का क्षेत्रफल = Δ I B C का क्षेत्रफल + Δ I C A का क्षेत्रफल + Δ I A B का क्षेत्रफल$
$\Rightarrow 24 = \frac{1}{2} (B C \times r) + \frac{1}{2} (C A \times r) + \frac{1}{2} (A B \times r)$
$\Rightarrow 24 = \frac{1}{2} r (B C + C A + A B)$
$\Rightarrow 24 = \frac{1}{2} \times r \times (10 + 8 + 6)$
$\Rightarrow 24 = 12 r$ ltbbrgt $\Rightarrow r = 2$

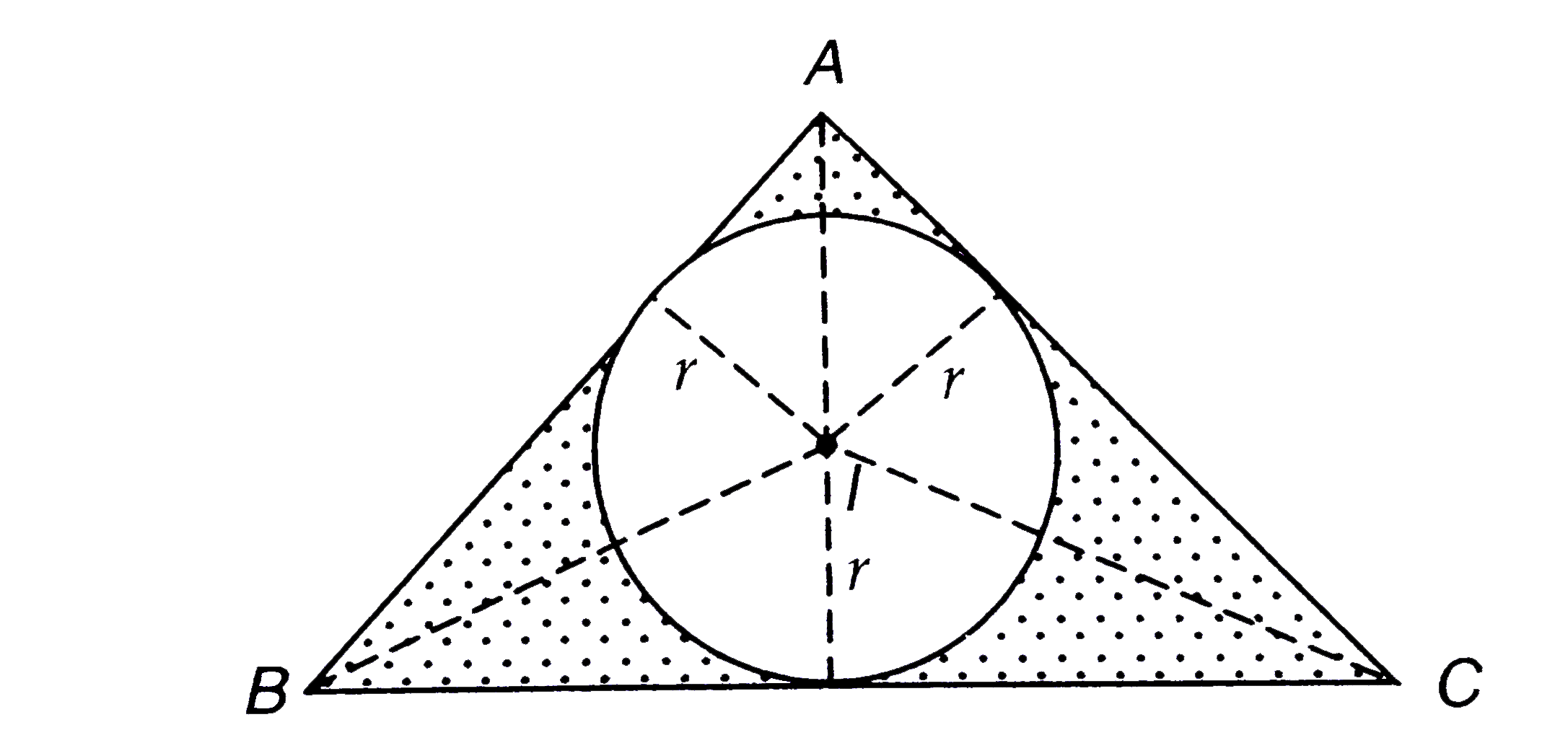
$∴$ छायांकित भाग का क्षेत्रफल $= Δ A B C$ का क्षेत्रफल - अंत:वृत्त का क्षेत्रफल
$\Rightarrow$ छायांकित भाग का क्षेत्रफल $= 24 - π r^{2} = (24 - \frac{22}{7} \times 4) {सेमी.}^{2} = \frac{80}{7} {सेमी.}^{2}$

Updated on:21/07/2023

|

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

RD SHARMA-वृत्तों से सम्बन्धित क्षेत्रफल -बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile