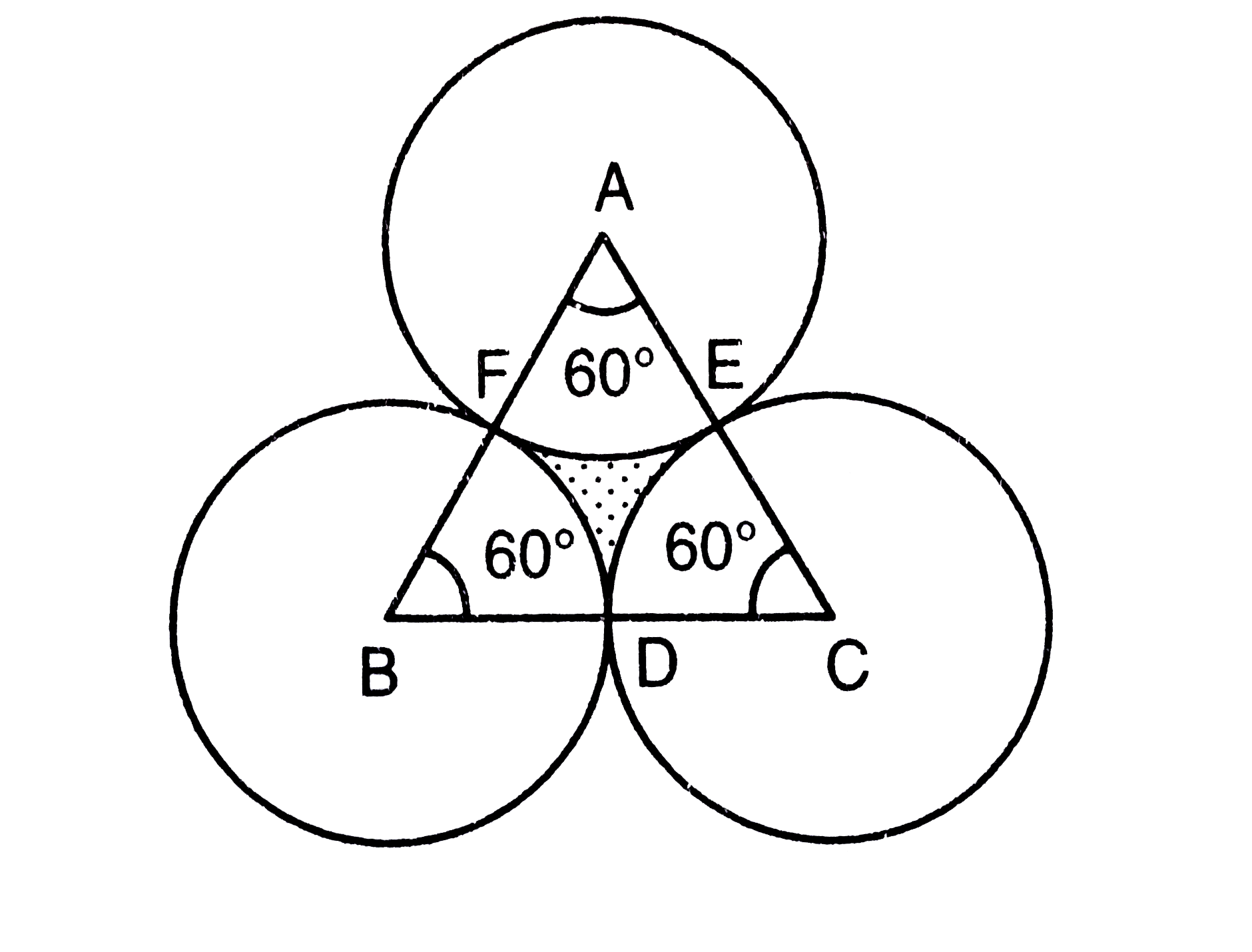
एक समबाहु त्रिभुज का क्षेत्रफल $1732.05 {सेमी.}^{2}$ है | इस त्रिभुज के प्रत्येक शीर्ष को केन्द्र मानकर, त्रिभुज की भुजा की लम्बाई के आधे के बराबर त्रिज्या लेकर वृत्त खींचे गये हैं | त्रिभुज का वह क्षेत्रफल ज्ञात कीजिये जो वृत्तों में सम्मिलित नहीं हैं | $(π = 3.14)$

Video Solution

Text Solution

Verified by Experts

माना समबाहु त्रिभुज की प्रत्येक भुजा a सेमी. है |
दिया है : त्रिभुज का क्षेत्रफल $= 1732.05 {सेमी.}^{2}$

$\Rightarrow \frac{\sqrt{3}}{4} a^{2} = 1732.05$
$\Rightarrow \frac{a^{2}}{4} = \frac{1732.05}{\sqrt{3}}$
$\Rightarrow {(\frac{a}{2})}^{2} = \frac{1732.05}{\sqrt{3}} ... (i)$
स्पष्ट है कि प्रत्येक वृत की त्रिज्या $\frac{a}{2}$ है |
मान लीजिये $\frac{a}{2}$ सेमी. त्रिज्या वाले वृत्त में $60^{\circ}$ कोण वाले त्रिज्यखण्ड का क्षेत्रफल A है |
$∴ A = 3 {\frac{60}{360} \times 3.14 \times {(\frac{a}{2})}^{2}} {सेमी.}^{2}$
$\Rightarrow A = \frac{1}{2} \times 3.14 \times {(\frac{a}{2})}^{2}$
$\Rightarrow \frac{1}{2} \times 3.14 \times \frac{1732.05}{\sqrt{3}} = 1570.04 {सेमी.}^{2} [(i) से {(\frac{a}{2})}^{2} = \frac{1732.05}{\sqrt{3}}]$
अत: अभीष्ट क्षेत्रफल
$= Δ A B C का क्षेत्रफल - \frac{a}{2} त्रिज्या वाले वृत्त में 60^{\circ} कोण वाले तीन त्रिज्यखण्डों का क्षेत्रफल$
$= (1732.05 - 1570.04) {सेमी.}^{2} = 162.01 {सेमी.}^{2}$

Updated on:21/07/2023

|

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

RD SHARMA-वृत्तों से सम्बन्धित क्षेत्रफल -बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile