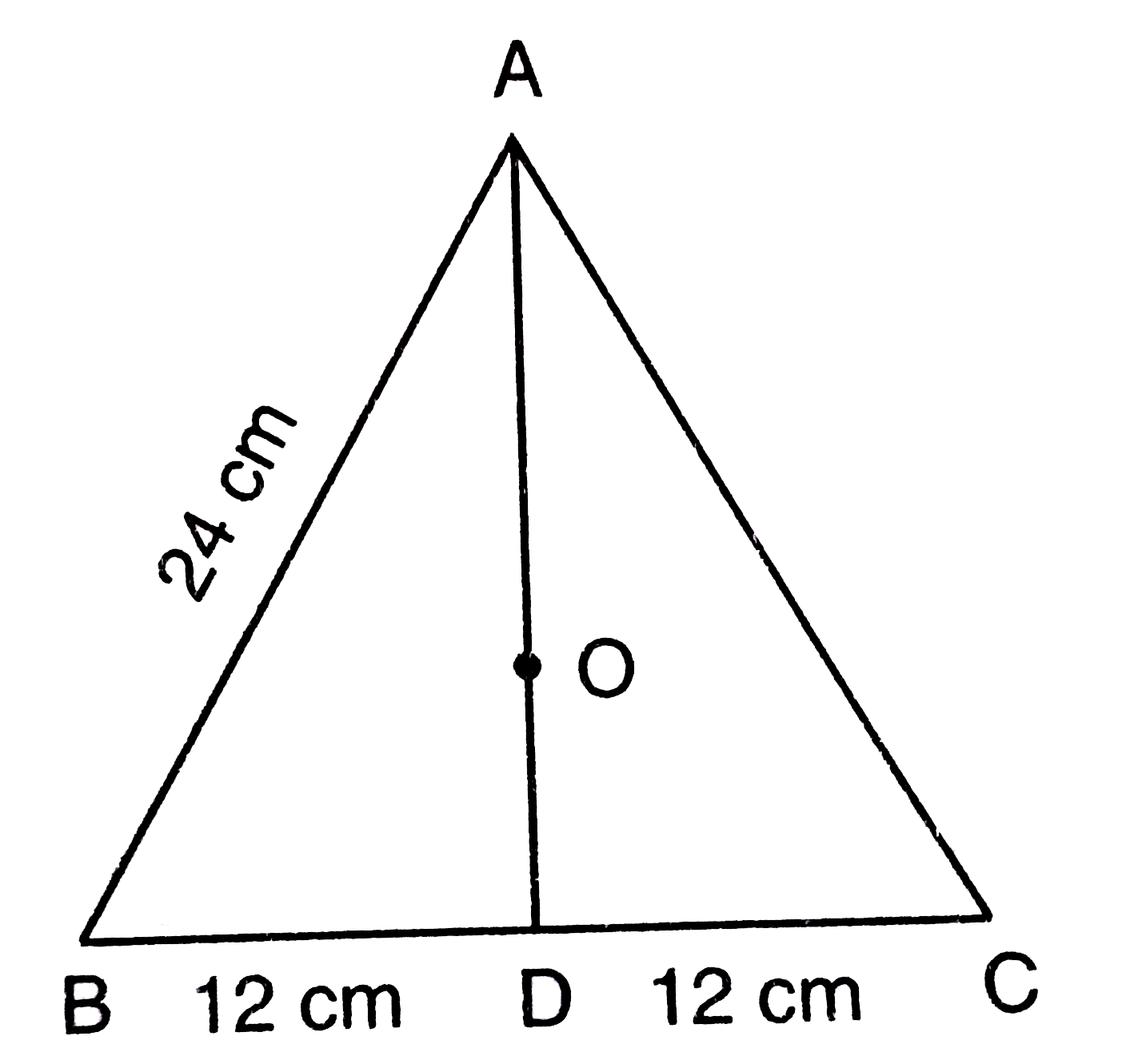
24 सेमी. भुजा वाले एक समबाहु त्रिभुज में, इसकी भुजाओं को स्पर्श करता हुआ एक अन्त:वृत्त बनाया गया है | त्रिभुज के शेष भाग का क्षेत्रफल ज्ञात कीजिये | (दिया है : $\sqrt{3} = 1.732$ )

Video Solution

Text Solution

Verified by Experts

माना कि ABC, 24 सेमी. भुजा वाला एक समबाहु त्रिभुज है तथा A से BC पर लम्ब AD है | चूँकि त्रिभुज समबाहु है इसलिये D, BC को समद्विभाजित करता है |
$∴ B D = C D = 12$
अन्त:वृत्त का केन्द्र, त्रिभुज ABC के केन्द्रक के संपाती होगा |
$∴ O D = \frac{A D}{3}$
$Δ A B D$ में,
$A B^{2} + A D^{2} + B D^{2} [पाइथागोरस प्रमेय द्वारा]$
$\Rightarrow 24^{2} = A D^{2} + 12^{2}$
$\Rightarrow A D = \sqrt{24^{2} - 12^{2}} = \sqrt{(24 - 12) (24 + 12)} = \sqrt{36 \times 12} = 12 \sqrt{3}$ सेमी.
$∴ O D = \frac{1}{3} A D = (\frac{1}{3} \times 12 \sqrt{3}) सेमी. = 4 \sqrt{3} सेमी.$

अन्त:वृत्त का क्षेत्रफल $= π {(O D)}^{2} = {\frac{22}{7} \times {(4 \sqrt{3})}^{2}} {सेमी.}^{2} = (\frac{22}{7} \times 48) {सेमी.}^{2} = 150.85 {सेमी.}^{2}$
$Δ A B C$ का क्षेत्रफल $= \frac{\sqrt{3}}{4} {(भुजा)}^{2} = \frac{\sqrt{3}}{4} {(24)}^{2} = 249.4 {सेमी.}^{2}$
$∴$ त्रिभुज के शेष भाग का क्षेत्रफल $= (249.4 - 150.85) {सेमी.}^{2} = 98.55 {सेमी.}^{2}$

Updated on:21/07/2023

|

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

RD SHARMA-वृत्तों से सम्बन्धित क्षेत्रफल -बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile