दो वृत्त बाह्ययत: स्पर्श करते हैं | यदि इनके क्षेत्रफलों का योग 130π वृत्त सेमी. है तथा इनके केंद्रों के बीच की दूरी 14 सेमी. है, तो इन वृत्तों की त्रिज्यायें ज्ञात कीजिए |
हम जानते हैं की यदि दो वृत्त बाहयतः स्पर्श करते हैं, तो उनके केन्द्रों के बीच की दूरी उनकी त्रिज्याओं के योगफल के बराबर होती है |
मान लीजिये C1 तथा C2 दिये गये वृत्तों के केन्द्र हैं और इनकी इनकी त्रिज्यायें क्रमश: r1 और r2 हैं | चूँकि दोनों वृत्त बाह्यत : स्पर्श करते हैं |
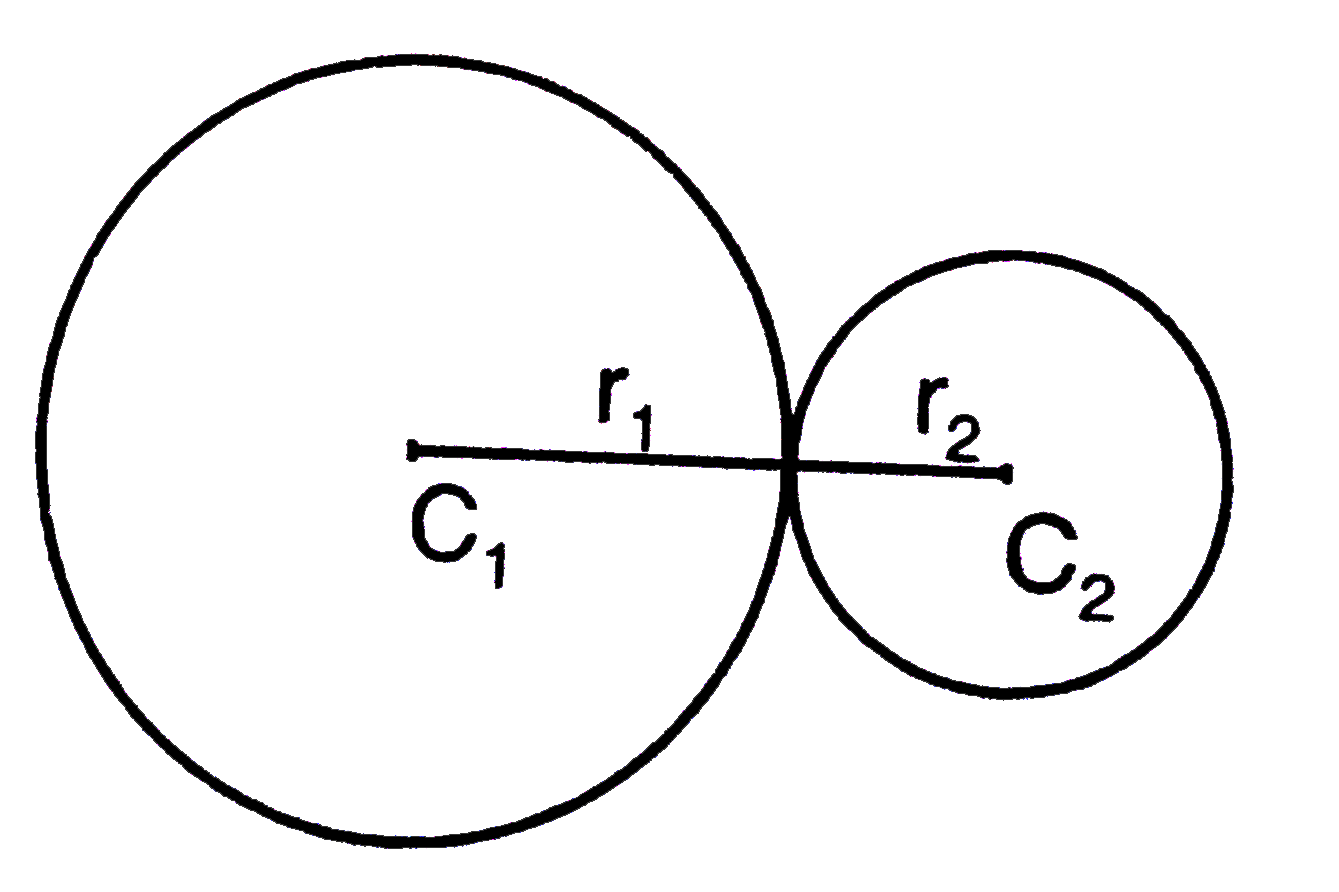
∴ C1C2=r1+r2
⇒ 14=r1+r2 [∵C1C2=14 सेमी. (दिया है)]
⇒ r1+r2=14 ...(i)
यह दिया है कि दोनों वृत्तों के क्षेत्रफलों का योगफल 130π सेमी.2 है |
∴ πr21+πr22=130π
⇒ r21+r22=130 ...(ii)
अब, (r1+r2)2=r21+r21+2r1r2
⇒ 142=130+2r1r2 [(i) तथा (ii) का प्रयोग करने पर]
⇒ 196−130=2r1r2
⇒ r1r2=33 ...(iii)
अब, (r1−r2)2=r21+r22−2r1r2
⇒ (r1−r2)2=130−2×33 [(iii) तथा (iv) का प्रयोग करने पर]
⇒ (r1−r2)2=64
⇒ r1−r2=8 ...(iv)
समीकरण (i) तथा (iv) को हल करने पर, r1=11 सेमी. तथा r2=3 सेमी.
अत: दोनों वृत्तों की त्रिज्यायें 11 सेमी. तथा 3 सेमी. हैं |
Topper's Solved these Questions
- वृत्तों से सम्बन्धित क्षेत्रफल Book:RD SHARMAChapter:वृत्तों से सम्बन्धित क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 19 Videos
- वृत्तों से सम्बन्धित क्षेत्रफल Book:RD SHARMAChapter:वृत्तों से सम्बन्धित क्षेत्रफल Exercise:प्रश्नावली 15.2
Explore 26 Videos
- वृत्त Book:RD SHARMAChapter:वृत्त Exercise:बहु विकल्पीय प्रश्न
Explore 15 Videos
- समान्तर श्रेढ़ी Book:RD SHARMAChapter:समान्तर श्रेढ़ी Exercise:बहु विकल्पीय प्रश्न
Explore 35 Videos
Similar Questions
4.2 सेमी. त्रिज्या वाले वृत्त की परिधि और क्षेत्रफल ज्ञात कीजिए |
View Solution4 सेमी. त्रिज्या वाले वृत्त के केन्द्र पर 30∘ का कोण आन्तरित करने वाली चाप की लम्बाई π के पदों में ज्ञात कीजिए |
View Solutionएक 5 सेमी त्रिज्या वाले वृत्त बिंदु पर स्पर्श रेखा PQ वृत्त के केंद्र O से जाने वाली रेखा को Q पर इस प्रकार काटती है कि OQ=12 सेमी है। PQ=
View Solutionयदि एक समांतर श्रेढ़ी का 7 वाँ तथा 13 वाँ पद क्रमश : 34 तथा 64 है , तो इसका 18 वाँ पद है :
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionदो वृत्त जिनकी त्रिज्याएँ क्रमशः 2.5 सेमी एवं 1.5 सेमी है जिनके केंद्र 8 सेमी दूरी पर स्थित है ,पर एक उभयनिष्ठ तिर्यक स्पर्श रेखा किन रचना कीजिए।
View Solutionदो वृत्त जिसकी त्रिज्याएँ 3 सेमी एवं 4 सेमी है। जिनके केन्द्रो के बाध्य की दूरी 8 सेमी है। दोनों वृतो पर उभयनिष्ठ स्पर्श रेखाएं कीतिनि खींची जा सकती है ?तथा दो उभयनिष्ठ अनुस्पर्श रेखाओ की रचना कीजि।
View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
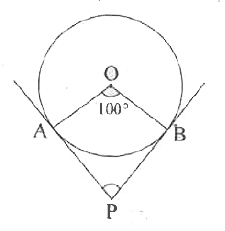
View Solutionकिसी वृत्त की जीवा AB द्वारा केंद्र पर अंतरित कोण 140∘ है तो A तथा B बिन्दुओ पर खींची गयी स्पर्श रेखाओ के बीच का कोण ज्ञात कीजिए।
View Solutionकिसी बाह्य बिंदु से वृत्त पर खींची गयी स्पर्श रेखा की लम्बाई 12 सेमी है ,यदि वृत्त की त्रिज्या 5 सेमी तो केंद्र से बाह्य बिंदु की दुइ ज्ञात कीजिए।
View Solutionदो वृत्त 2.5 सेमी एवं 1 सेमी त्रिजियो के केंद्र परस्पर 7 सेमी दूरी पर है। एक उभयनिष्ठ तिर्यक स्पर्श रेखा कि रचना कीजिए।
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि वृत्त के केंद्र से 3 सेमी. की दूरी पर स्थित जीवा की लम्बाई 8 सेमी. है, तो वृत्त की त्रिज्या ज्ञात कीजिए।
View SolutionPQ and RS are two chords, of a circle. PQ =20 cm, RS =48 cm and PQ is parallel to RS. If the distance between PQ and RS is 34 cm, then what is the area (in cm^2 ) of the circle? PQ तथा RS एक वृत्त की 2 जीवाएं हैं। PQ=20 सेमी., RS =48 सेमी. तथा PQ,RS के समानान्तर है। यदि PQ तथा RS के मध्य दूरी 34 सेमी. है, तो वृत्त का क्षेत्रफल ( सेमी.^2 ) क्या है?
View SolutionThe distance between the centres of two circles is 24 cm. If the radius of the two circles are 4cm and 8cm, then what is the sum of the lengths (in cm) of the direct common tangent and the transverse common tangent? दो वृत्तों के केन्द्र के मध्य की दूरी 24सेमी. है। यदि दो वृत्त की त्रिज्या 4 सेमी. तथा 8 सेमी है, तो उभयनिष्ठ अनुस्पर्श रेखा तथा तिर्यक उभयनिष्ठ अनुस्पर्श रेखा की लम्बाई (सेमी. में) का योग क्या है?
View SolutionIf the length of a chord of a circle C at a distance of 12 cm from the centre is 10 cm, then the diaimeter of the circle is यदि किसी वृत्त के केन्द्र से 12 सेमी. की दूरी पर जीवा की लंबाई 10 सेमी. है, तो वृत्त का व्यास है-
View Solution

