(i) Draw the plot of amplitude versus ω for an amplitude modulated were whose carrier wave (ωc) is carrying two modulating signals, ω1 and ω2 (ω2>ω1).
(ii) Is the plot symmetrical about ωc ? Comment especially about plot in region ω<ωc.
(iii) Extrapolate and predict the problems one can expect if more waves are to be modulated.
(iv) Suggest solutions to the above problem. In the process can one understand another advantage of modulation in terms of bandwidth?
(i) Let the two modulating signals Am1sinωm1t and Am2sinωm2t be superimposed on carrier signal
Acsimωct. The signal produced is x(t)=Am1sinωm1t+Am2sinωm2t+Acsinωct
To produce amplitude modulated wave the signal x(t) is passed through a square law device which produces
an output given by
y(t)=B[Am1sinωm1+Am2sinωm2t+Acsinωct]+C[Am1sinωm1t+Am2sinωm2t+Acsimωct]2
B=[Am1sinωm1t+Am2sinωm2t+Acsinωct]+C[(Am1sinωm1t+Am2sinωm2t)2+A2csin2ωct
+2Acsinωct(Am1sinωm1t+Am2sinωm2t)]
=B[Am1sinωm1t+Am2sinωm2t+Acsinωct]
+C[A2m1sin2ωm1t+A2m2sin2ωm2t+2Am1Am2sinωm1tsinωm2t
+A2csim2ωct+2Ac(Am1sinωm1tsinωct+Am2sinωm2tsinωct)]
=B[Am1sinωm1t+Am2sinωm2t+Acsinωct]
+C[A2m1sin2ωm1t+A2m2sin2ωm2t+Am1Am2{cos(ωm2−ωm1)t−cos(ωm2+ωm1)}+A2csin2ωct
+AcAm1{cos(ωc−ωm1)t−cos(ωc+ωm1)t}+AcAm2{cos(ωc−ωm2)t−cos(ωc+ωm2)t}]
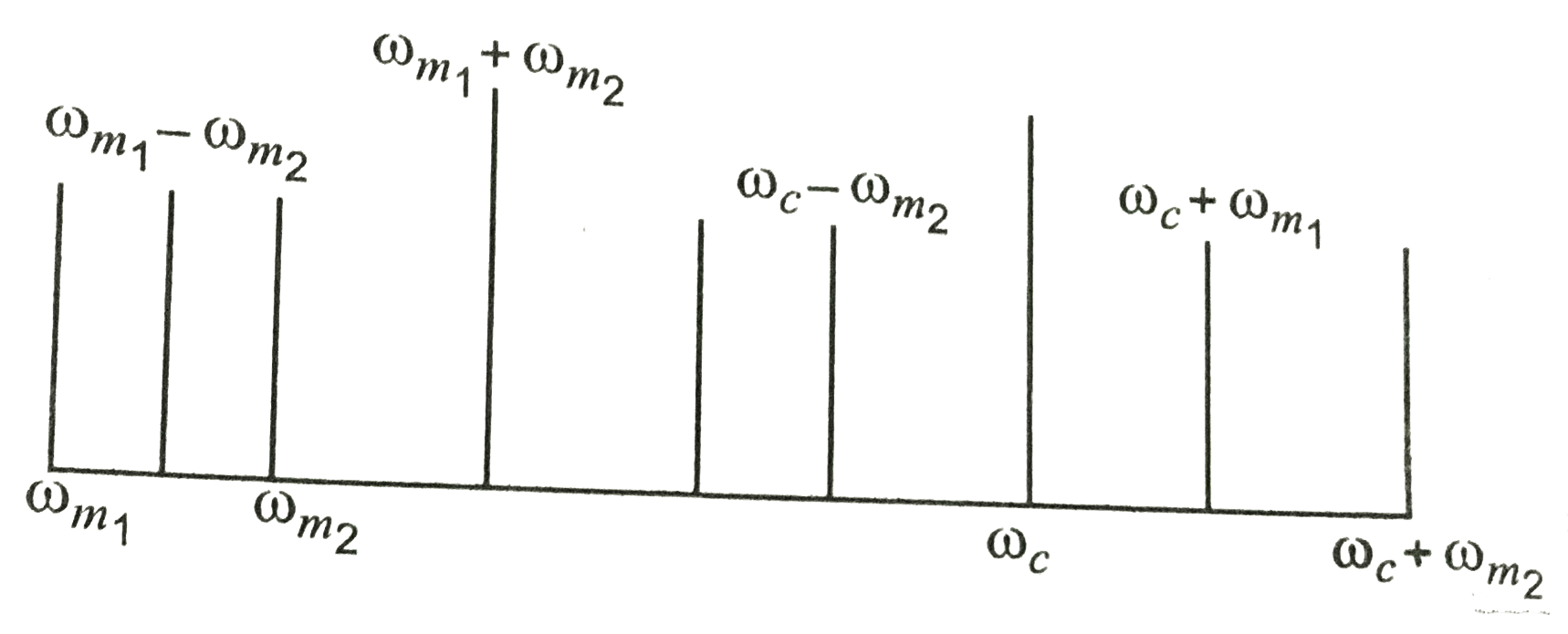
In the above amplitude modulated waves, the frequencies present are
ωm1,ωm2,ωc,(ωm2−ωm1),(ωm2+ωm1),(ωc−ωm1),(ωc+ωm1),(ωc−ωm2) and (ωc+ωm2)
The plot of amplitude versus ω is shown in
figure
(ii) From figure , we note that frequency
spectrum is not symmetrical about ωc.
Crowding of spectrum is present for ω<ωc.
(iii) if more waves are to be modulated then
there will be more crowding in the modulating
signal in the region ω<ωc. That will result
more chances of mixing of signals.
(iv) To accommodate more signals, we should increase band width and frequency of carrier waves ωc. This
shows that large carrier frequency enables to carry more information (i.e., more ωm) and the same will
inturn increase band width.
Topper's Solved these Questions
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:HIGHER ORDER THINKING SKILLS
Explore 2 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:Value Based Questions
Explore 4 Videos
- COMMUNICATION SYSTEMSBook:PRADEEPChapter:COMMUNICATION SYSTEMSExercise:NCERT EXERCISES
Explore 1 Video
- ATOMS AND NUCLEIBook:PRADEEPChapter:ATOMS AND NUCLEIExercise:Assertion- Reason type question 12
Explore 1 Video
- CURRENT ELECTRICITYBook:PRADEEPChapter:CURRENT ELECTRICITYExercise:Problems for Practice (B)
Explore 2 Videos
Similar Questions
(i) Draw the plot of amplitude versus ω for an amplitude modulated were whose carrier wave (ωc) is carrying two modulating signals, ω1 and ω2 (ω2>ω1).
(ii) Is the plot symmetrical about ωc ? Comment especially about plot in region ω<ωc.
(iii) Extrapolate and predict the problems one can expect if more waves are to be modulated.
(iv) Suggest solutions to the above problem. In the process can one understand another advantage of modulation in terms of bandwidth?
View Solution∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣
View Solution
Knowledge Check
If ω is cube root of unity, then ∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣ is equal to
A1BωCω2D0If two independent waves are y1=a1sinω1 and y2=a2sinω2t then
Athey will not produce interference.Bthey will produce interferenceCthey may or may not produce interference.Dit is difficult to comment about the result.Equation of messages signal m=2sinωm(t) and carrier signal c=4sinωC(t). The equation of modulating signal will be
A4sinωC(t)+2sinωm(t)B4sinωC(t)+2sinωm(t)⋅sinωC(t)C8sinωC(t)+sinωm(t)D(1+sinωm(t))sinωm(t)
(a+bω+cω2)(a+bω2+cω)
View Solution∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣=
View Solution(1−ω+ω2)(1+ω−ω2)=4
View SolutionA message signal A1sinω1 t is used to modulate the amplitude of a carrier wave A2sinω2t, where A1<A2andω2>>ω1. What is the modulation index of the modulated waye ?
View Solution∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣
View Solution

