A transparent paper (refractive index = 1.45) of thickness 0-02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed ?
The correct Answer is:14.5
From y0=βλ(μ−1)
No. of fringes that cross when paper is removed
=y0β=(μ−1)tλ=(1.45−1)×0.02×10−3620×10−9
=14.5
Topper's Solved these Questions
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Problems for practice
4 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Comprehension 1
1 Videos
- OPTICSBOOK - PRADEEPCHAPTER - OPTICSEXERCISE - Value based questions
3 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBOOK - PRADEEPCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Competition Focus (Multiple Choice Questions)
2 Videos
Similar Questions
A transparent paper (μ=1.45) of thickness 0.023 mm is pasted on one of the sdlits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross the centre if the paper is removed ?
View SolutionA transparent sheet of thickness 0.018 mm is pasted on one of the slits of a Youngs slit experiment. If the set - up uses monochromatic light of wavelength 6800Å, how many fringes will shift due to pasting of the sheet? Take μ sheet = 1.6.
View Solution
Knowledge Check
In Young's double slit experiment with monochromatic light of wavelength 600 nm, the distance between slits is 10−3m. For changing fringe width by 3×10−5m
Athe screen is moved away from the slits by 5cmBthe screen is moved by 5 cm towards the slitsCthe screen is moved by 3 cm towards the slitsDboth (a) and (b) are correct.If a transparent medium of refractive index μ=1.5 and thickness t=2.5×10−5m is inserted in front of one of the slits of Young's Double Slit experiment, how much will be the shift in the interference patten? The distance between the slits is 0.5mm and that between slits and screen is 100cm
A(a) 5cmB(b) 2.5cmC(c) 0.25cmD(d) 0.1cmIn Young's double slit experiment, the fringe width with light of wavelength 6000 Ã… is 3 mm. The fringe width, when the wavelength of light is changed to 4000 Ã… is
A3 mmB1 mmC2 mmD4 mm
Find the angular fringe width in Young's double slit experiment using a monochromatic light of wavelength 500 nm when the slits are separated by 2.5 mm.
View SolutionOn placing a thin film of mica of thickness 12×10−5cm in the path of one of the interfering beams in young's double slit experiment using monochromatic light, the fringe pattern shifts through a distance equal to the width of a bright fringe. If λ=6×10−5cm, the refractive index of mica is
View SolutionIn Young's double slit experiment, the fringe width obtained by a monochromatic light of wavelength 6000Å is 2 mm. I fthe apparatus is dipped into water of R.I. 1:33, then change in fringe width will be
View SolutionThe figure shows the interference pattern obtained in a double-slit experiment using light of wavelength 600 nm.
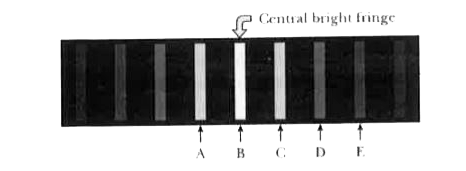
Which fringe is the same distance from both slits?
View SolutionWhat will happen if one of the slits in Young's double slit experiment is covered with cellophane paper which absorbs a fraction of the intensity of light from the slit?
View Solution
