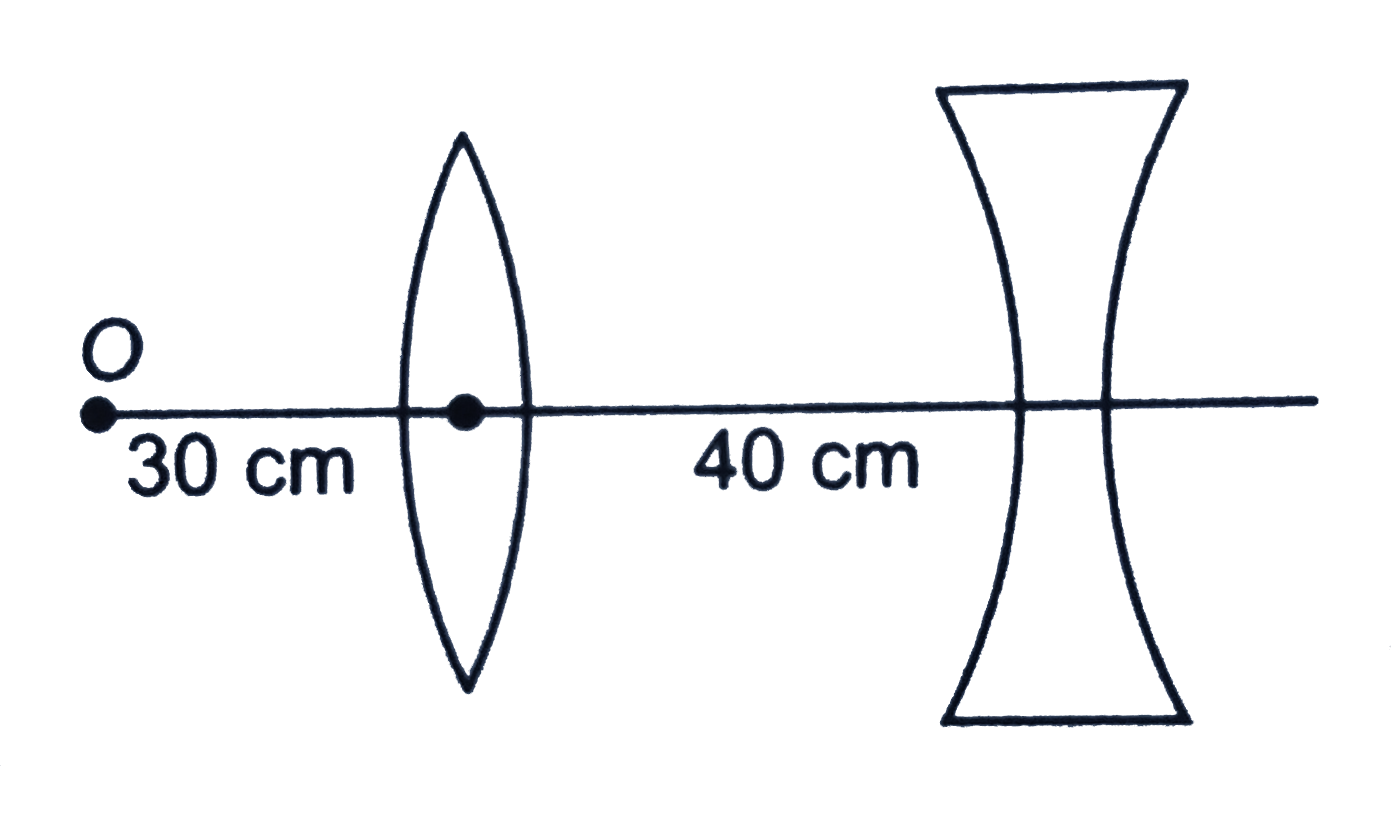
Rays of light are falling on a convex lens of focal length 40cm. As shown in Fig. Determine the position of the image.
 .
.
The correct Answer is:8cm
f=+40cm,u=+10cm,v=?
1v=1f+1u=140+110=540=18
v=8cm
Topper's Solved these Questions
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Problems for practice
Explore 4 Videos
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Comprehension 1
Explore 1 Video
- OPTICSBook:PRADEEPChapter:OPTICSExercise:Value based questions
Explore 3 Videos
- MAGNETIC EFFECT OF CURRENT AND MAGNETISMBook:PRADEEPChapter:MAGNETIC EFFECT OF CURRENT AND MAGNETISMExercise:Competition Focus (Multiple Choice Questions)
Explore 2 Videos
Similar Questions
Find the power of a convex lens of focal length 40 cm.
View SolutionConverging light rays are falling on a convex lens. If the focal length of the lens is 30 cm, then find the position of the image.
View SolutionA 1.0-cm-high object is placed at a distance of 12 cm from a convex lens of focal length 16 cm. Find the position of the image.
View SolutionAn object is placed at a distance of 30 cm from a convex lens of focal length 20 cm.Find the position of the image .
View SolutionAn object is placed at 10 cm from a convex lens of focal length 12 cm. Find the position, nature and magnification of the image.
View SolutionAn object 4 cm high is placed at a distance of 10 cm from a convex lens of focal length 20 cm. Find the position, nature and size of the image.
View SolutionA convex lens of focal length 30 cm is placed coaxially in contact with a concave lens of focal length 40 cm. Determine the power of the combination. Will the system be converging or diverging in nature?
View SolutionAn object 3 cm high is placed 20 cm from convex lens of focal length 12 cm. Find the nature, position and height of the image.
View SolutionFocal length of a convex lens in air is 20cm. and of concave lens 40cm. Find the position of final image.
View SolutionIf an object of 7 cm height is placed at a distance of 12 cm from a convex lens of focal length 8 cm, find the position, nature and height of the image.
View Solution

