The radii of curvature of each surface of a convex lens is $20 c m$ and the refractive index of the material of the lens is $3 / 2$ (i) Calculate its focal length (ii) If this is cut along the plane $A B$ . What will be formed ? (iii) What happens if the lens is cut along $C D$ ?

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $20 c m; 40 c m; 20 c m$

(i) $\frac{1}{f} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{R_{2}})$
$= (\frac{3}{2} - 1) (\frac{1}{20} + \frac{1}{20}) = \frac{1}{20}$ ,
$f = 20 c m$
(ii) When lens is cut along the plane $A B$ , Fig. focal length of each half is given by
$\frac{1}{f} = (μ - 1) (\frac{1}{R_{1}} - \frac{1}{\infty}) = (\frac{3}{2} - 1) \times \frac{1}{20} = \frac{1}{40}$
$f_{1} = 40 c m$

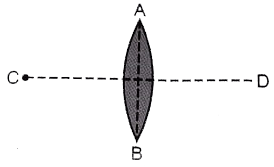
(iii) When lens is cut along $C D$ , Fig. each half continues to have original focal length $f = 20 c m$ . However, intensity of image will reduce.

|

Updated on:21/07/2023

Class 12 PHYSICS GEOMETRICAL OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The radius of curvature of the curved surface of a plano-convex lens is $20 c m$ . If the refractive index of the material of the lens be $1.5$ , it will
Aact as a convex lens only for the object that lie on its curved side.
Bact as a concave lens for the objects that lie on its curved side.
Cact as a convex lens irrespective of the side on which the object lies.
Dact as a concave lens irrespective of side on which the object lies.
Question 2 - Select One
The radius of curvature of the curved surface of a plano-convex lens is $20 c m$ . If the refractive index of the material of the lens be $1.5$ , it will
A $30 c m$
B $50 c m$
C $20 c m$
D $40 c m$
Question 3 - Select One
The radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
A6cm
B12cm
C18cm
D24cm

PRADEEP-OPTICS-Exercise

Home
Ask Doubt
Profile