(a) Fig shows a capacitor made of two circular plates each of radius 12cm and separated by 5.0mm. The capacitor is being charged by an external source (not shown in the figure). The charging current is constant and equal to 0.15A. Use Ampere's law (modified to include displacement current as given in the text) and the symmetryin the problem to calculate magnetic field between the plates at a point (i) on the axis (ii) 6.5 cm from the axis (iii) 15cm from the axis.
(b) At what distance from the axis is the magnetic field due to displacement current greatest? Obtain the maximum value of the field.

Text Solution

Verified by Experts

Here, $R = 0.12 m, I = 0.15 A$
$∴$ Area of the plate, $A = π R^{2} = π \times {(0.12)}^{2} m^{2}$
(a) Consider a loop of radius r between the two
circular plates, placed coaxially with them.
Then area of the loop, $A' = π r^{2}$
By symmetry magnetic field induction $\to B$ is
equal in magnitude and is tangentially to the circle
at every point.
In this. only displacement current $I_{D}$ will
cross the loop. Therefore, using Ampere's Maxwell
law, we have
$\oint \to B . \to d l = μ_{0} I_{D}$
$2 π r B = μ_{0} \times$ (current passing
through the area A')
$= μ_{0} I_{D} \frac{π r^{2}}{π R^{2}}$ for $r < R$
$= μ_{0} I_{D}$ for $r > R$
Thus, $B = \frac{μ_{0} I_{D} r^{2}}{R^{2} 2 π r} = \frac{μ_{0} I_{D} r}{2 π R^{2}}$ ....(i) (If $r < R)$
and $B = \frac{μ_{0} I_{D}}{2 π r}$ ....(ii) (If $r > R)$
(i) On the axis, $r = 0$
Using (i), we get, $B = 0$
(ii) For a point 6.5cm from the axis,
$r = 6.5 c m = 6.5 \times 10^{- 2} m$ .
Using (i), we have,
$B = \frac{4 π \times 10^{- 7} \times 0.15 \times 6.5 \times 10^{- 2}}{2 π \times {(12 \times 10^{- 2})}^{2}}$
$= 1.35 \times 10^{- 7} T$
(iii) For a point 15 cm from the axis,
$r = 15 c m = 0.15 m$ .
Using (ii), we have
$B = \frac{4 π \times 10^{- 7} \times 0.15}{2 π \times 0.15} = 2 \times 10^{- 7} T$
(b) From equation (i) and (ii) we note that B
is maximum if $r = R = 12 c m = 0.12 m$
$∴ B_{max} = \frac{μ_{0} I_{D}}{2 π R} = \frac{4 π \times 10^{- 7} \times 0.15}{2 π \times 0.12}$
$= 2.5 \times 10^{- 7} T$

Updated on:21/07/2023

A capacitor made of two circular plates each of radius 12 cm and separated by 5 mm. The capacitor is being charged by an external source. The charging current is constant and equal to 0.15 A. The capacitance of the parallel plate capacitor is

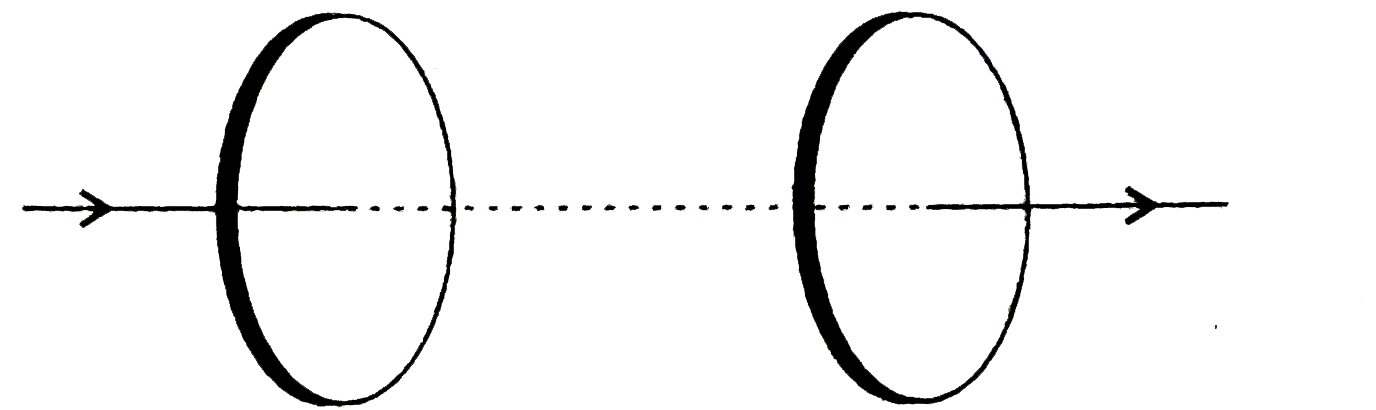A40 pF
B45 pF
C70 pF
D80 pF
A capacitor made of two circular plates each of radius 12 cm and separated by 5 cm. The capacitor is being charged by an external source. The charging current is constant and equal to 0.15 A. The capacitance of the parallel plate capacitor is

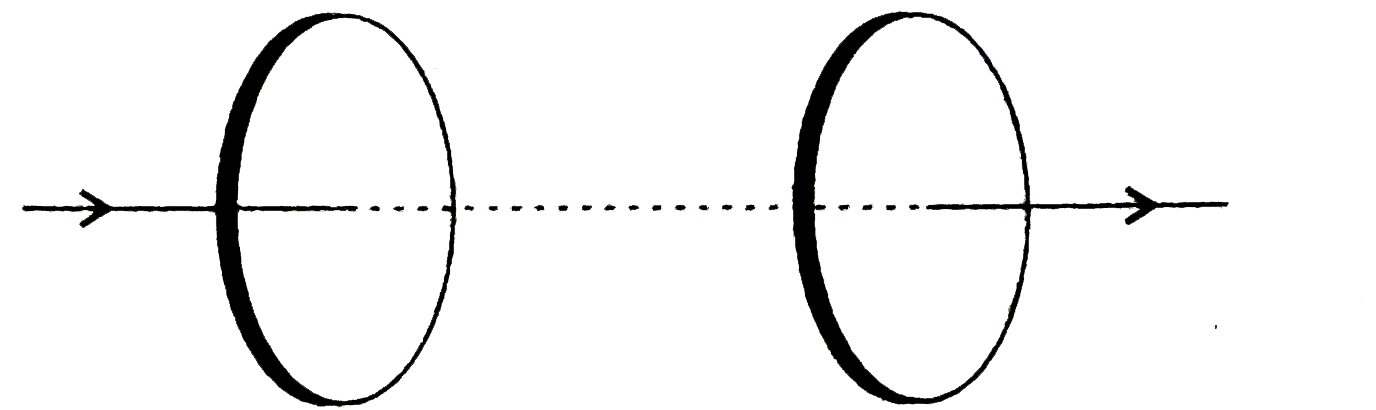A40 pF
B45 pF
C70 pF
D80 pF
A parallel plate capacitor consists of two circular plates each of radius $12 c m$ and separated by $5.0 m m$ . The capacitor is being charge by an external source. The charging current is constant and is equal to $0.15$ A. The rate of change of potential difference between the plate will be
A $8.173 \times 10^{7} V s^{- 1}$
B $7.817 \times 10^{8} V s^{- 1}$
C $1.173 \times 10^{9} V c^{- 1}$
D $3.781 \times 10^{10} V s^{- 1}$