Consider a closed loop C in a magnetic field, Fig. The flux passing through the loop is defined by choosing a surface whose edge coincides with the loop and using the formula ϕ=B1.dA1+B2.Da2+……..Now if we chose two different surfaces S1 and S2 having C as their edge, would we get the same answer for flux. Justify your answer.
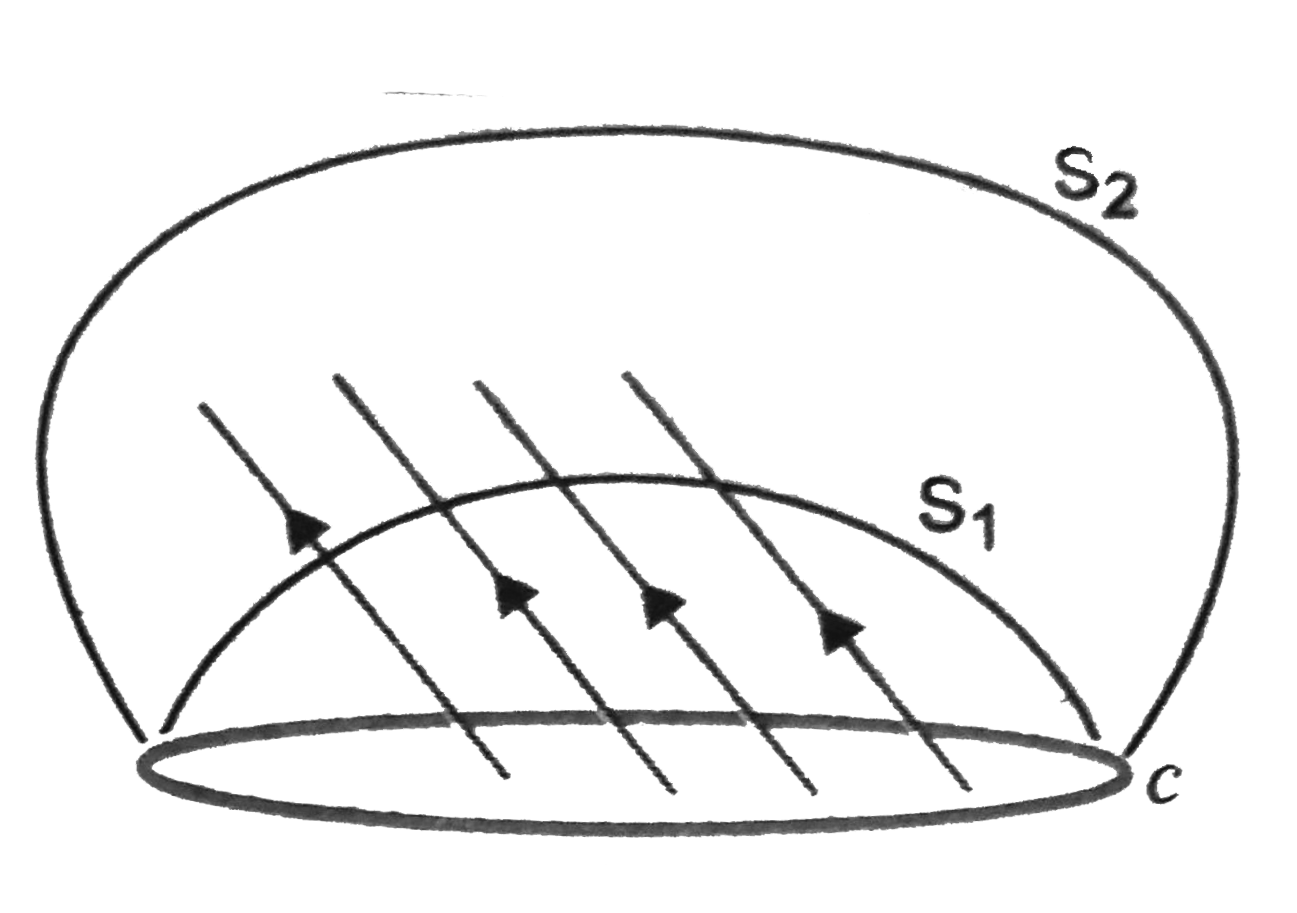
We would get the same answer for magnetic flux. This is because magnetic flux = number of magnetic field lines passing through the surface (dϕ=→B.Δ→S). As magnetic field lines form closed continuos loops and cannot end or start in space, therefore in Fig. number of magnetic lines passing through surface S1 must be the same as the number of magnetic lines through the surface S2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Solved Examples (b)
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Short Answer Qusetions
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:II Focus multiple choice question
Explore 5 Videos
Similar Questions
The current through the solenoid is changing in such way that flux through it is given by ϕ=ɛ t .The solenoid is surrounded by a loop having resistance R1 and R2 as shown.Then the reading of the two voltmeters V1 and V2 differ by :
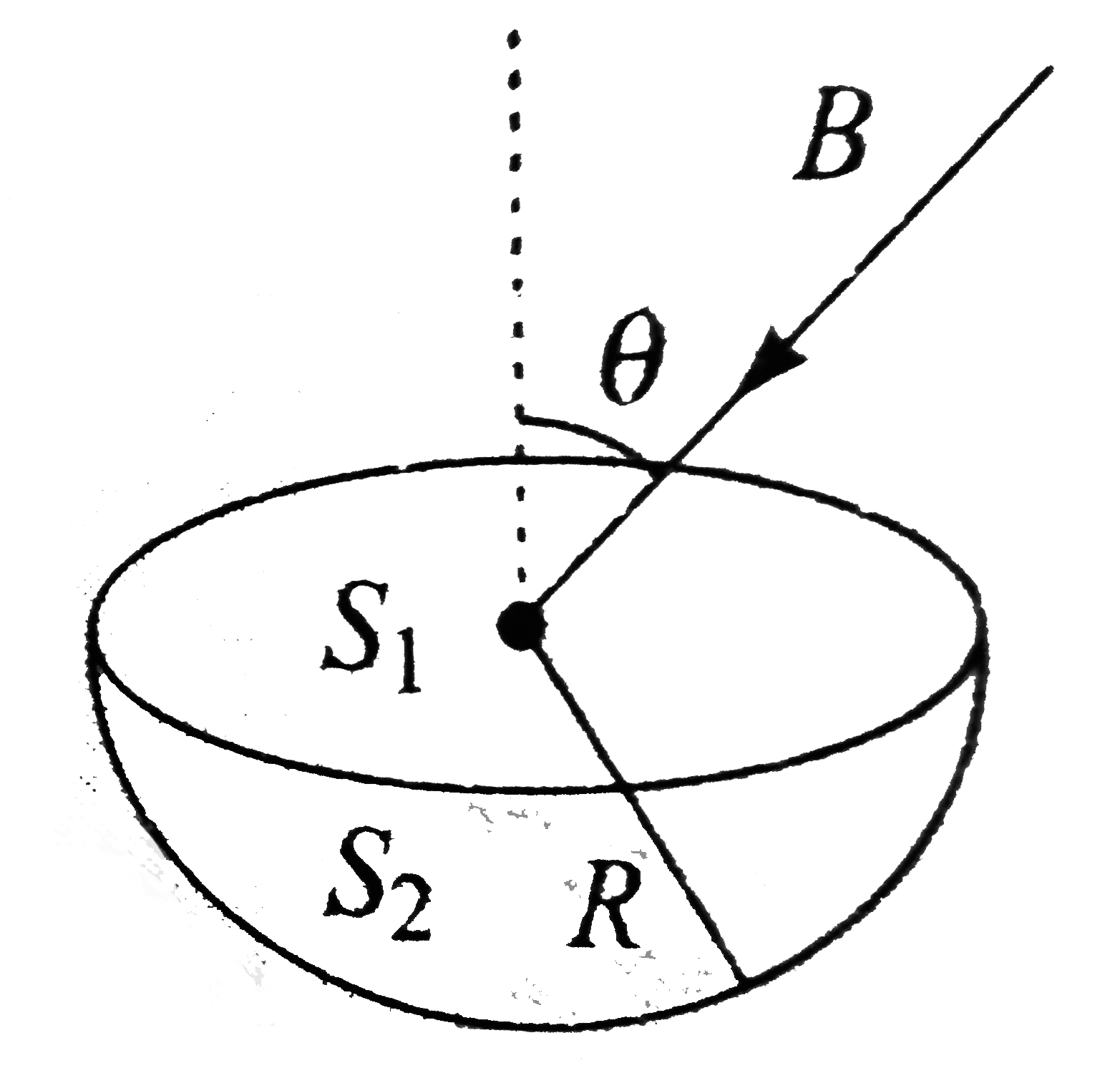
View SolutionConsider the hemispherical closed surface as shown in Fig. 3.19. if the hemisphere is a uniform magnetic field that makes an angle θ with the vertical, calculate the magnetic flux
(a) through the flat surface S1.
(b) through the hemisphere surface S2.
View Solution
Knowledge Check
The magnetic flux across a loop of resistance 10Ω is given by ϕ=(5t2−4t2+1)Wb. How much current is induced in the loop after 0.2 s?
A0.4 AB0.2 AC0.04 AD0.02 AA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
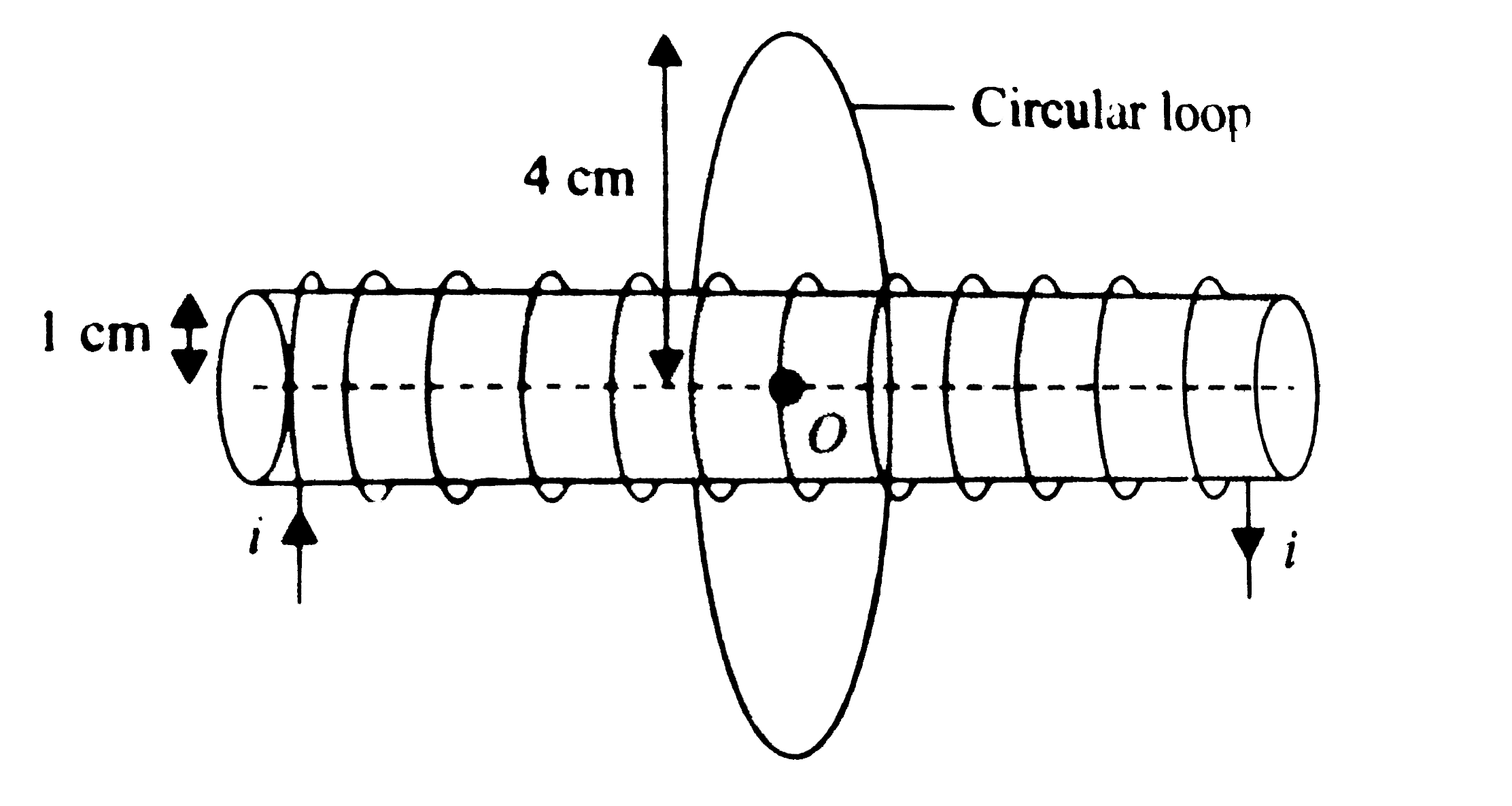
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.A4.7×10−7Vm−1B3.82×10−6Vm−1C2.3×10−5Vm−1DNone of theseA square non - conducting loop , 20 cm , on a side is placed in a magnetic field . The centre of side AB coincides with the centre of magnetic field . The magnetic field is increasing at the rate 2 T /s . The potential difference betweeen B and C is :
 A30 m VBzeroC10 mVD20 m V
A30 m VBzeroC10 mVD20 m V
Consider a closed surface of arbitatry shape as shown in figure. Suppose a single charge Q1 is located at some point within the surface and second charge Q2 is located outside the surface.

a. What is the total flux passing through the surface due to charge Q1?
b. What is the total flux passing through the surface due to charge Q2?
View SolutionThe flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ=at2+bt+c. (a) Write the SI units of a,b and c. (b) if the magnitudes of a,b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
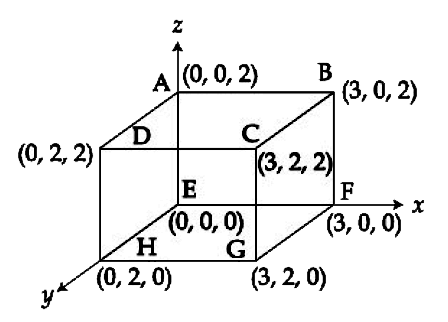
View SolutionAn electric field →E=4xˆi−(y2+1)ˆjN/C passes through the box shown in figure. The flux of the electric field through surface ABCD and BCGF are marked as ϕ1)andϕ11 respecticvely. The differentce between (ϕ1−ϕ1) is in Nm2/C)
View SolutionFigure shows four charges q1,q2,q3,andq4 fixed is space. Then the total flux of the electric field through a closed surface S, due to all the charges, is

View SolutionA loop of area 1m2 is placed in a magnetic field B=2T, such that plane of the loop is parallel to the magnetic field. If the loop is rotated by 180∘, the amount of net charge passing through any point of loop, it its resistance is 10Ω is
View Solution
