The output E of an alternating voltage supply of frequency 50 Hz is shown in Fig. From this Fig, state
(i) value of time $t_{1}$
(ii) peak voltage $E_{0}$ (iii) root mean square voltage $E_{v}$
(iv) mean supply is connected in series with a resistance of $2.4 Ω$ , calculate the mean power dissipated in the resistor.

Video Solution

Text Solution

Verified by Experts

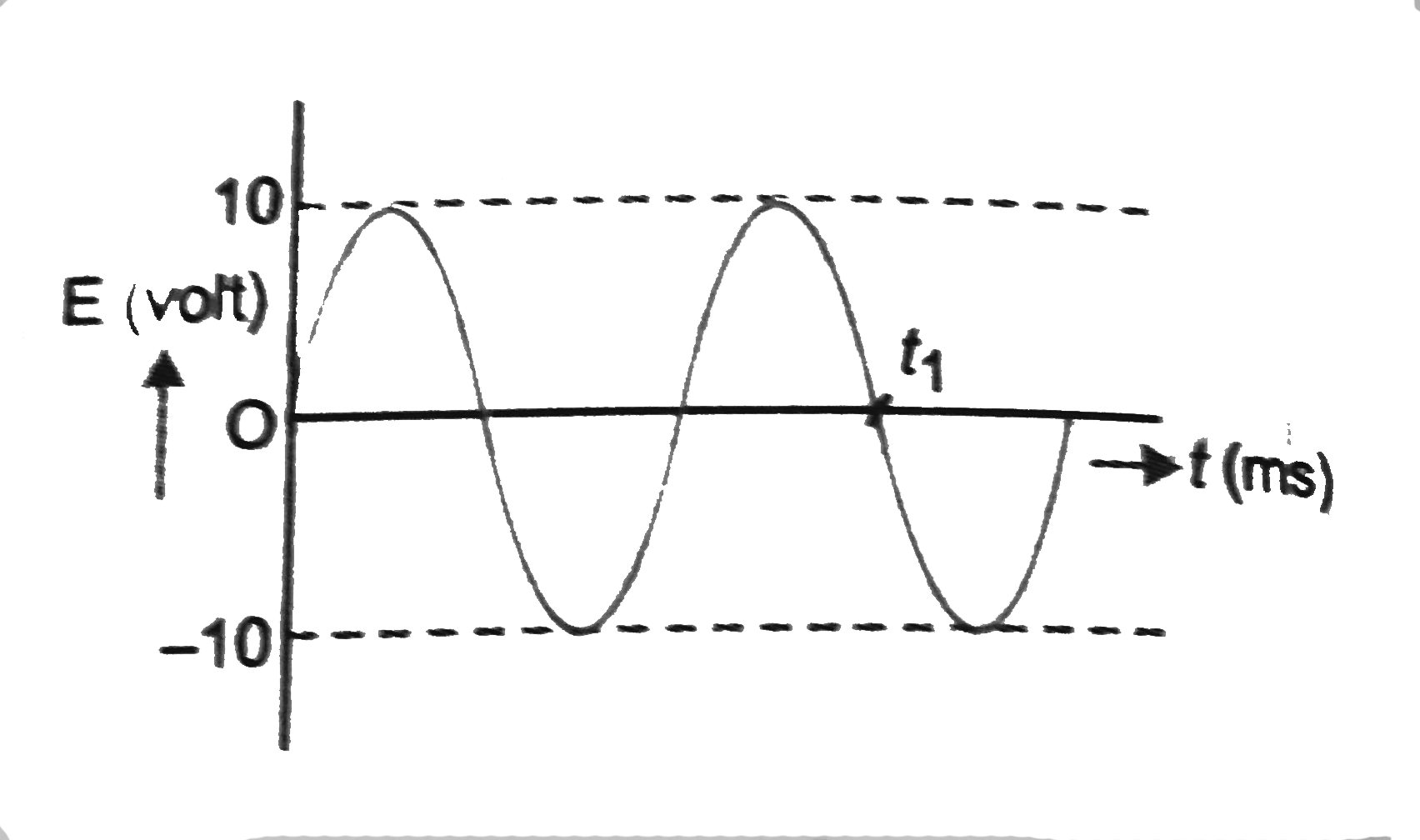
Here, $v = 50 H z, E_{0} = 10 V$
From Fig. we find that
$t_{1} = \frac{3}{2} T = \frac{3}{2 \times v} = \frac{3}{2 \times 50} = 0.03 s$
(ii) peak voltage = 10 V
(iii) $E_{v} = \frac{E_{0}}{\sqrt{2}} = \frac{10}{1.414} = 7.07$ volt
(iv) Mean averge voltage over full cycle = Zero. the mean power dissipated in the resistor
$E_{v} = \frac{E_{v}^{2}}{R} = \frac{10 {\sqrt{2}}^{2}}{2.4} = \frac{50}{2.4} = 20.83 W$

Updated on:21/07/2023

An alternating voltage is given by: $e = e_{1} sin ω t + e_{2} cos ω t$ . Then the root mean square value of voltage is given by:
A $\sqrt{e_{1}^{2} + e_{2}^{2}}$
B $\sqrt{e_{1} e_{2}}$
C $\sqrt{\frac{e_{1} e_{2}}{2}}$
D $\sqrt{\frac{e_{1}^{2} e_{2}^{2}}{2}}$
An alternating voltage is given by: $e = e_{1} sin ω t + e_{2} cos ω t$ . Then the root mean square value of voltage is given by:
A $\sqrt{e_{1}^{2} + e_{2}^{2}}$
B $\sqrt{e_{1} e_{2}}$
C $\sqrt{\frac{e_{1} e_{2}}{2}}$
D $\sqrt{\frac{e_{1}^{2} + e_{2}^{2}}{2}}$
A 10 ohm resistor is conneted to a supply voltage alternating between +4V and -2V as shown in the following graph. The average power dissipated in the resistor per cycle is

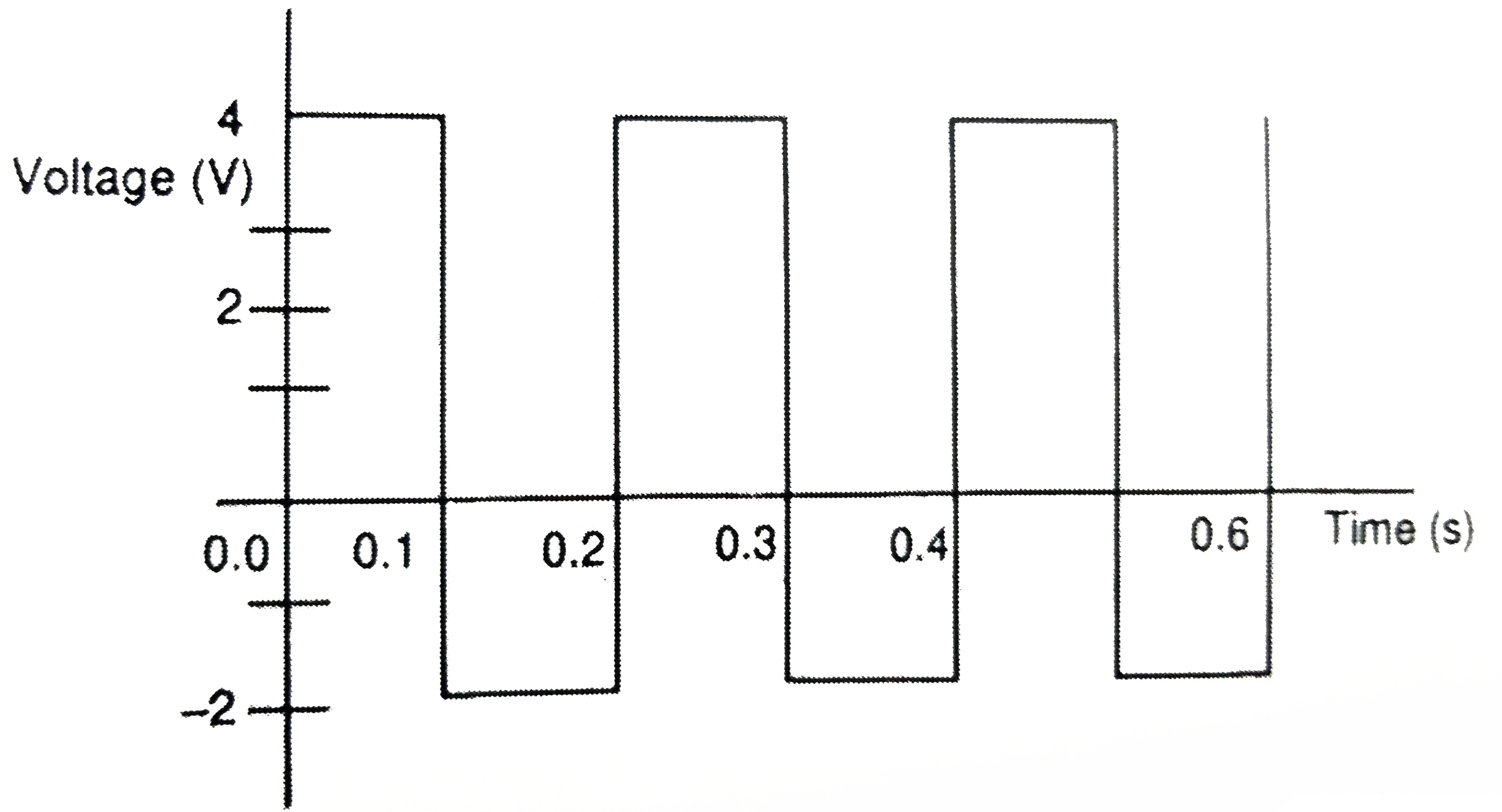A1.0 W
B1.2 W
C1.4 W
D1.6 W