Show that the sum of instantaneous currents during growth and decay of current in LR circuit is independent of time.
Video Solution
Text Solution
During growth of current in LR circuit,
Ig=I0(1−e−Rt/L) and
during decay of current in LR circuit,
Id=I0e−Rt/L
Sum of the currents at any instant t,
Ig+Id=I0(1−e−Rt/L+e−Rt/L)=I0
which is constant, and is independent to time.
|
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Solved Examples (b)
Explore 1 Video
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBook:PRADEEPChapter:ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTExercise:Short Answer Qusetions
Explore 2 Videos
- DUAL NATURE OF RADIATION AND MATTERBook:PRADEEPChapter:DUAL NATURE OF RADIATION AND MATTERExercise:Exercise
Explore 191 Videos
- ELECTROMAGNETIC WAVESBook:PRADEEPChapter:ELECTROMAGNETIC WAVESExercise:II Focus multiple choice question
Explore 5 Videos
Similar Questions
Knowledge Check
The dimensionsof "time constant" LR during growth and decay of current in all inductive circuit is same as that of
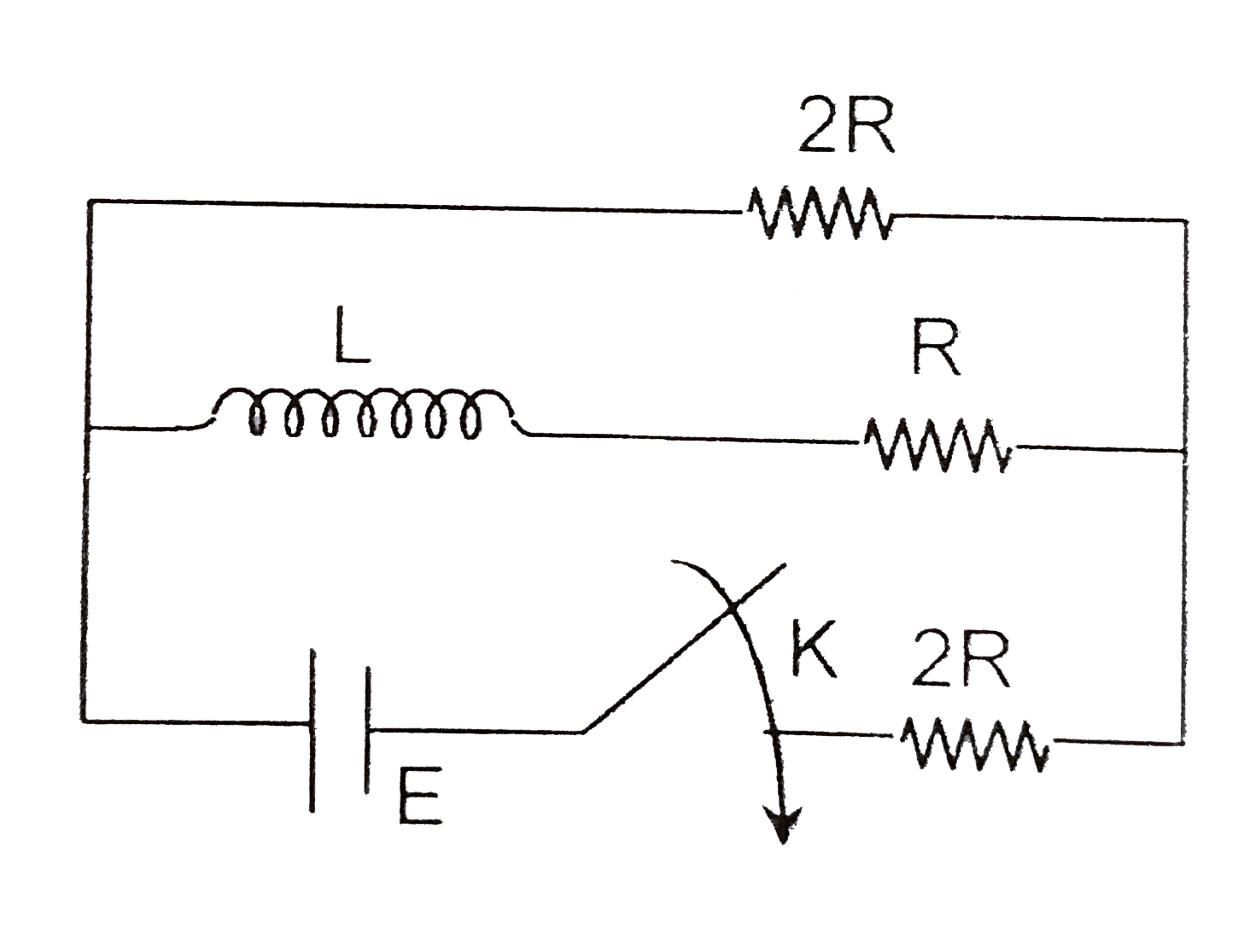
AConstantBResistanceCCurrentDTime
Current in the ain circuit shows isA1.5 AB0.083333333333333C0.6 AD1AThe ratio of time constant during current growth and current decay of the circuit shown in Figure is
 A1:1B3:2C2:3D1:3
A1:1B3:2C2:3D1:3