A block with mass (M) is connected by a massless spring with stiffness constant (k) to a rigid wall and moves without friction on a horizontal surface. The block oscillates with small amplitude A about an equilibrium position (x_0). Consider two cases : (i) when the block is at (x_0) , and (ii) when the block is at x=x0+A. In both the cases, a particle with mass m(lt M) is softly placed on the block after which they strick to each other. Which of the following statement (s) is (are) true about the motion after the mass (m) is placed on the mass (M) ?
The amplitude of oscillation in the first case changes by a factor of √Mm+M, whereas in the second case it remains unchanged .
The final time period of oscillation in both the cases is same.
The total energy decreases in both the cases.
The instantaneous speed at x0 of the combined masses decreases in both the cases.
The correct Answer is:A, B, D
When a block alonge oscillates on a horizontal frictionless surface, then its angular frequency of oscillation is, ω0=√kM
After a mass m is placed on block, the angular frequency of oscillation , ω=√km+M
Let υ′ be the velocity of the blocks (M+m), then using law of conservation of linear momentum,
we have
Mυ0=(M+m)υ′ or Mω0A=(M+m)ωA′
or A′A=M(M+m)×ω0ω
=M(M+m)×√k/M√k/(M+m)=√MM+m
At extreme position, the velocity of block,
υM=0 ltbr> When mass m is placed on block os mass M at extreme position,
velocity of block and mass m is , υM+m=0 ltbr> Therefore, the extreme position and mean position remain unchanged. Hence, A′=A.
Final time period of oscillation.
T′=2πω=2π√M+mk.
It is same in both the cases.
Total energy decreases in 1st case, but not in 2nd case.
Instantaneous velocity at x0,i.e.,
Velocity at mean position =ωA′.. It decrease ini both the cases.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - integer type question8videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Assertion-Reason Type Questions23videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II14videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
A block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:
View SolutionA block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1. At the instant when the block passes through its equilibrium position a lump of putty with mass m is dropped vertically on the block from a very small height and sticks to it.
(a) Find the new amplitude and period.
(b) Repeat part (a) for the case in which the putty is dropped on the block when it is at one end of its path.View Solution
Knowledge Check
- Question 1 - Select One
A 100g block is connected to a horizontal massless spring of force constant 25.6N/m. The block is free to oscillate on a horizontal fricationless surface. The block is displced by 3cm from the equilibrium position, and at t=0, it si released from rest at x=0, The position-time graph of motion of the block is shown in figure.
_S01_050_Q01.png)
When the block is at position A on the graph, itsAposition and velocity both are negativeBposition and velocity both are positive.Cposition is negative and velocity is positive.Dposition is positive and velocity is negative.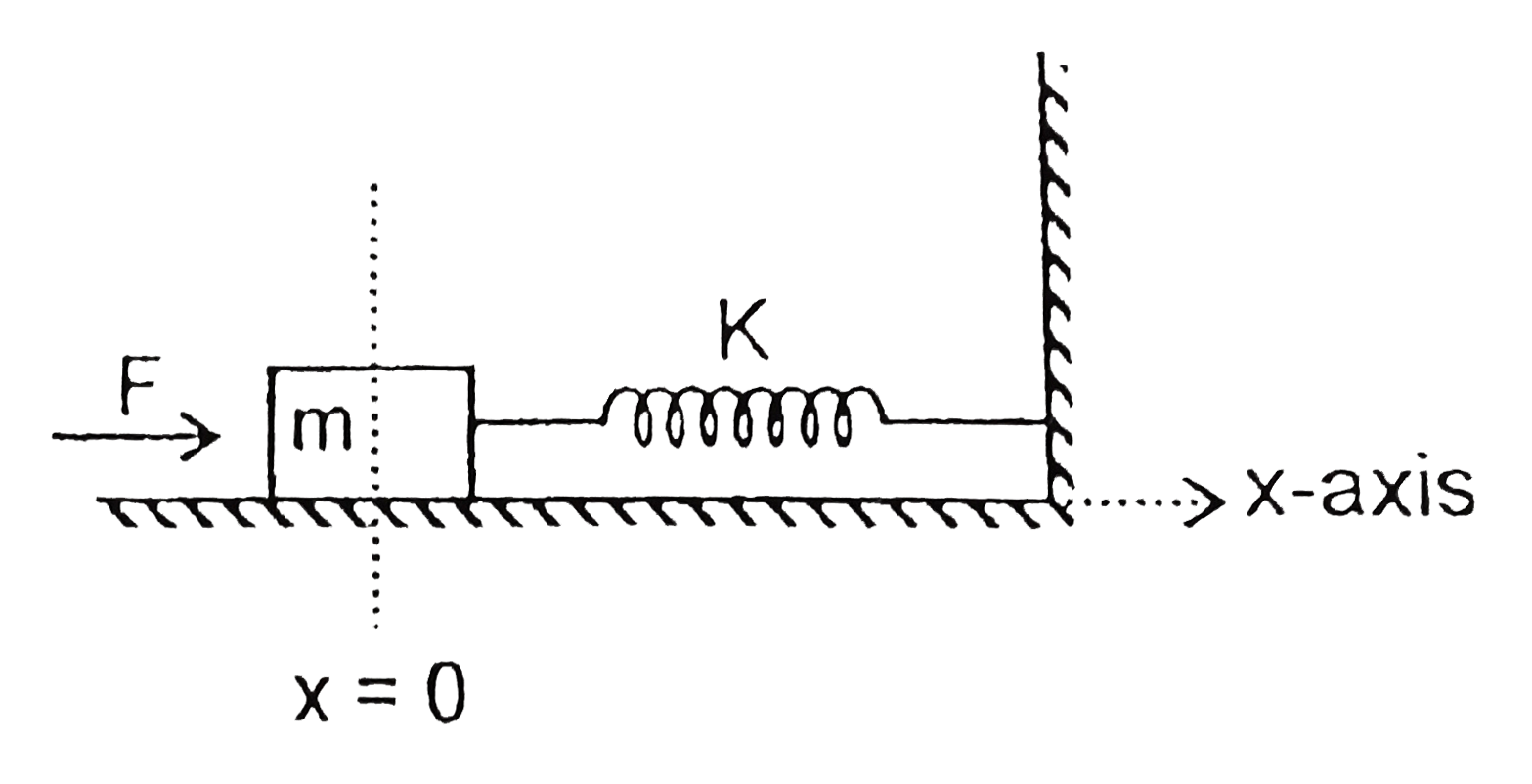 - Question 2 - Select One or More
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ thenAMotion of block is SHMBTime period of motion is π√mk[√2+√23]CTime period of motion is π√mk[1+√32]DSum of potential energy and kinetic energy of spring block system is maximum at right extreme. - Question 3 - Select One
One end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface There is another and wall at a distance x0 from the block The spring is then compressed by 2x0 and released The time taken to at the wall is
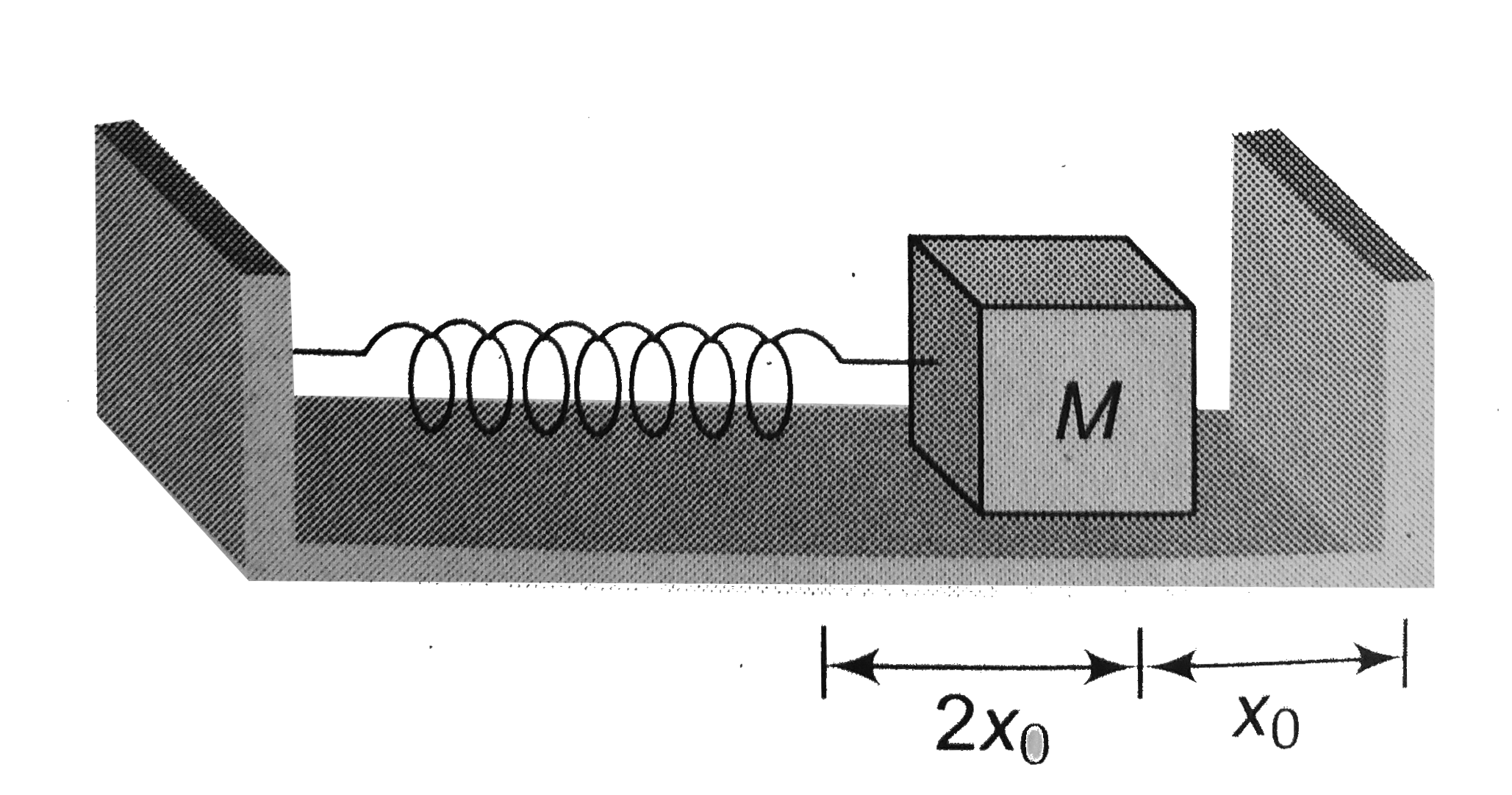A16π√kmB√kmC2π3√mkDπ4√km
A block of mass 1kg is connected with massless spring of constant 100N/m .At t=0 ,a constant force F=10N is applied on the block. The spring is in its natural length at t=0.The speed of particle at x=6cm form mean position is
View Solution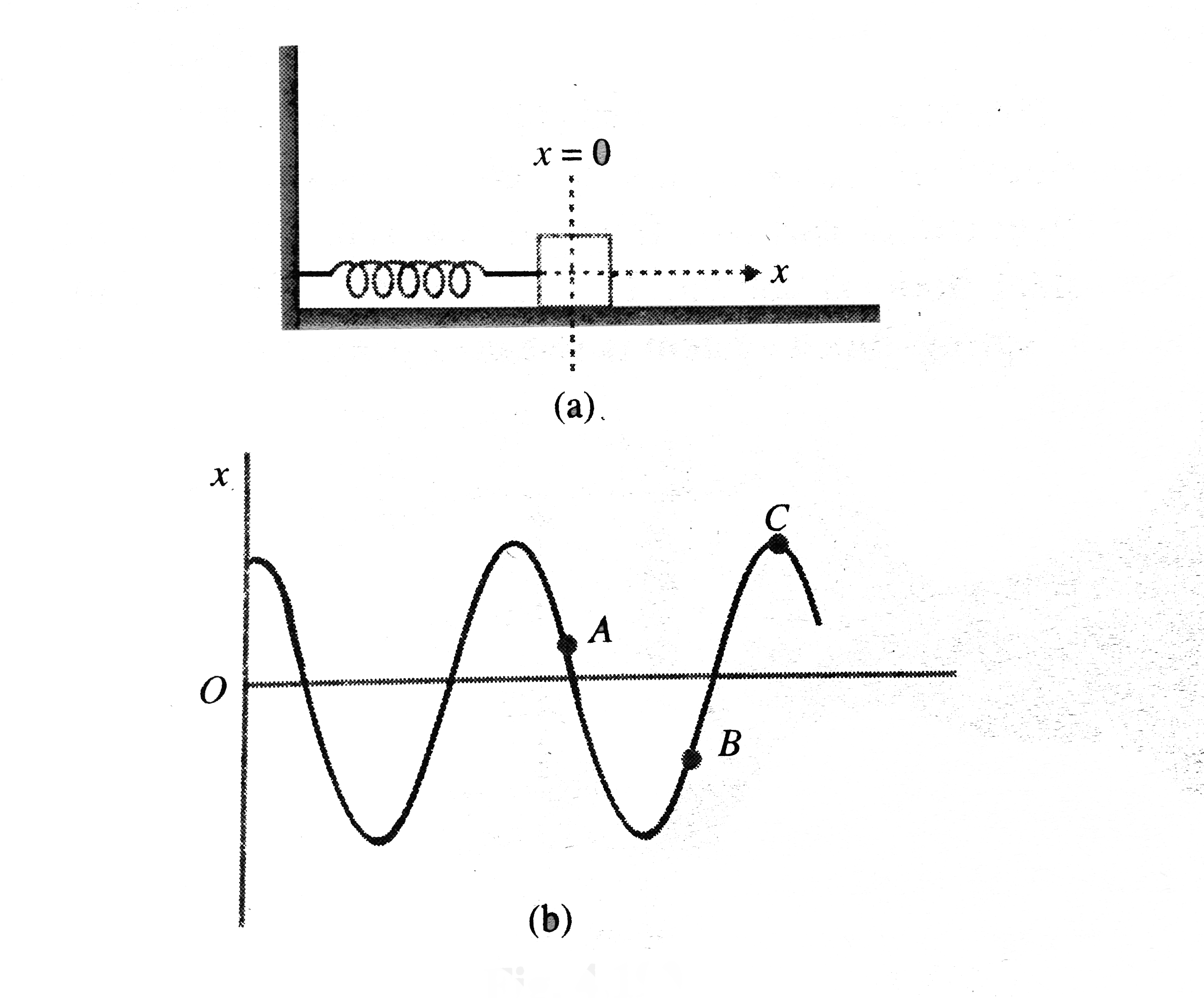
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
When the block is at position C on the graph, itsView SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View Solution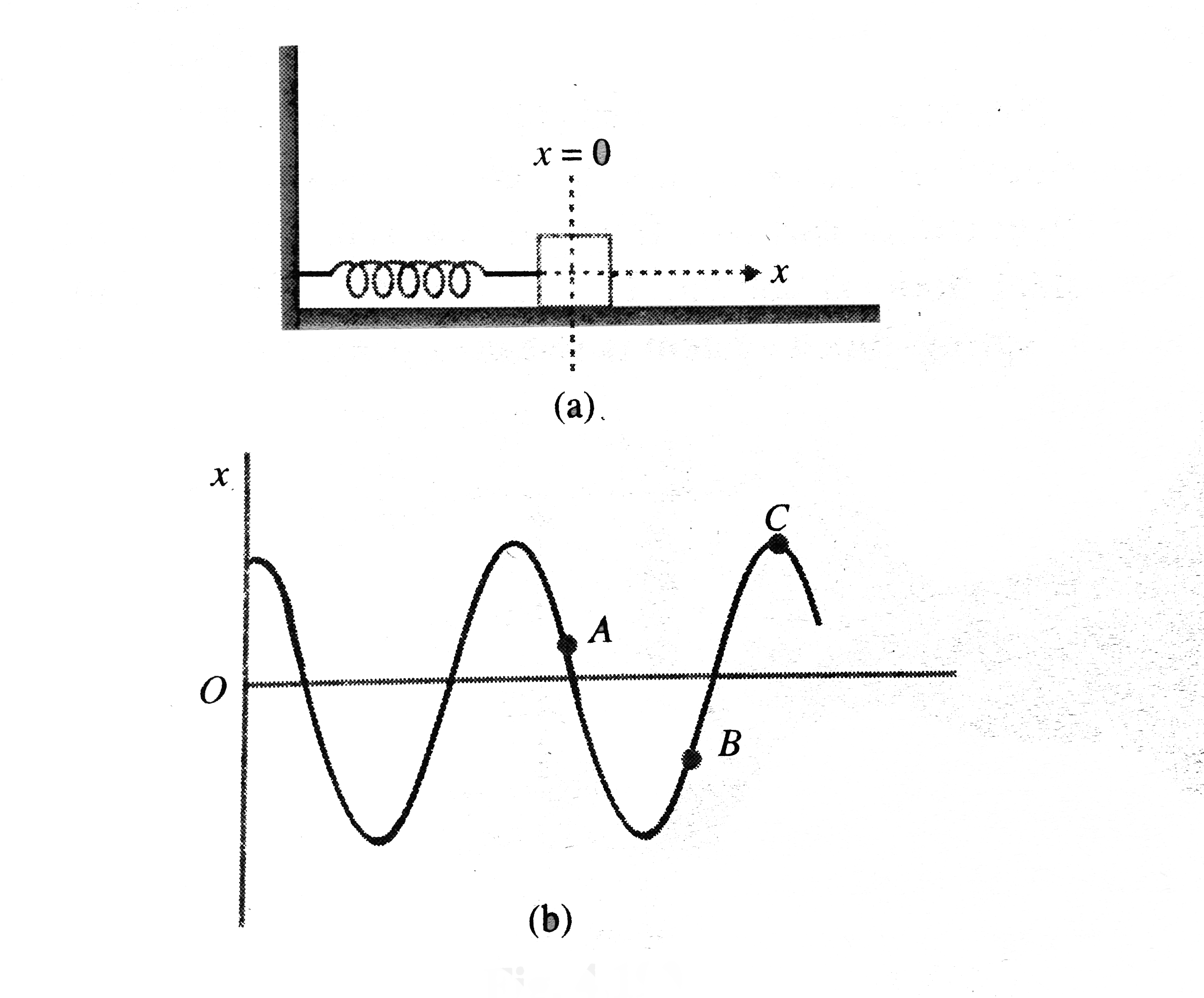
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x−direction∈decated∈Fig.Thepositiontime(x-t) graph of motion of the block is as shown in Fig.
Q. When the block is at position A on the graph, itsView Solution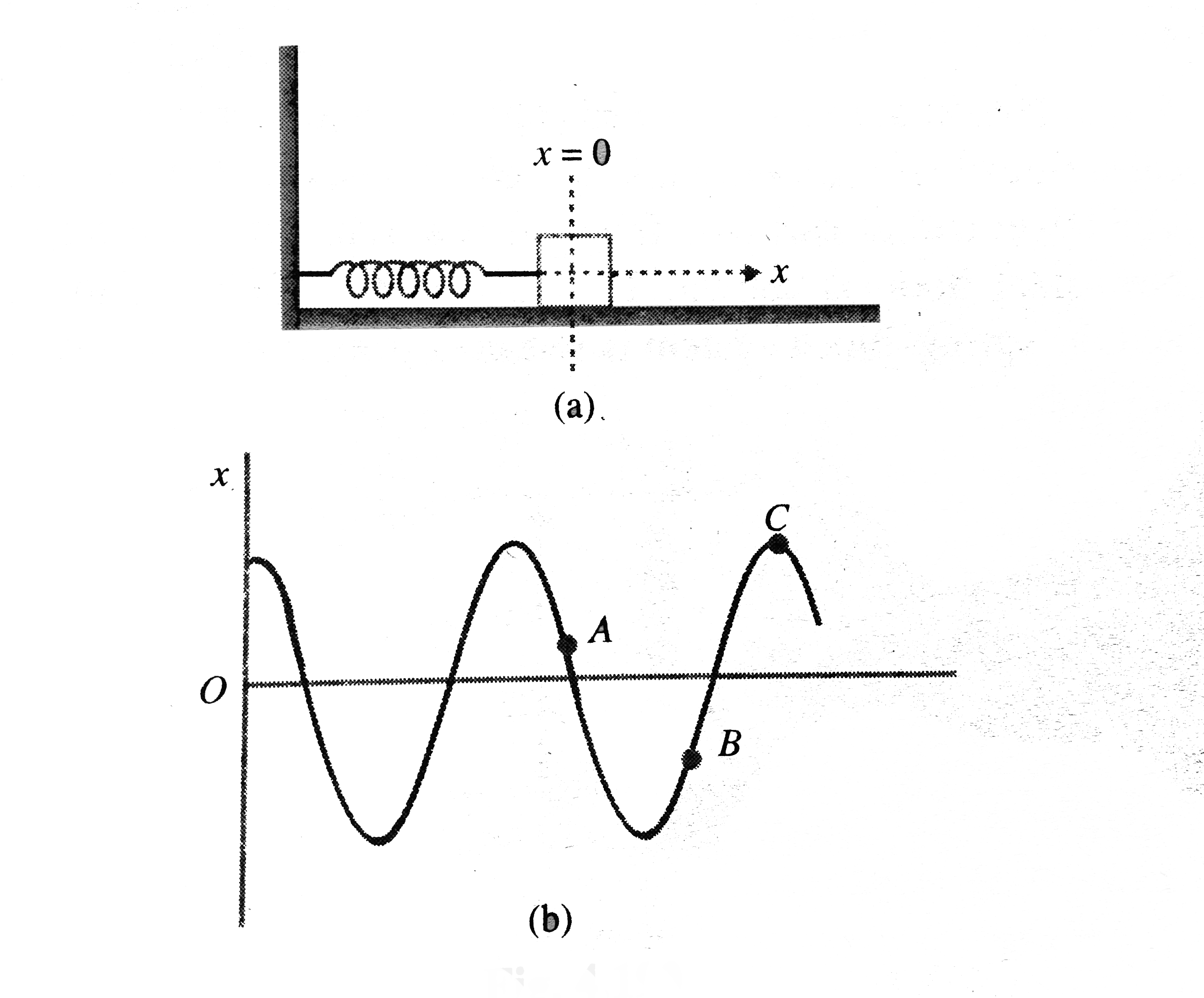
A 100 g block is connected to a horizontal massless spring of force constant 25.6Nm As shown in Fig. the block is free to oscillate on a horizontal frictionless surface. The block is displaced 3 cm from the equilibrium position and , at t=0, it is released from rest at x=0 It executes simple harmonic motion with the postive x-direction indecated in Fig. The position time (x−t) graph of motion of the block is as shown in Fig.
Q. When the block is at position B on the graph its.View Solution