If a simple pendulum has significant amplitude (up to a factor of1//e of original) only in the period between t−0s→t=τs, then τ may be called the average life of the pendulum. When the sphetical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity with b as the constant of propotional to average life time of the pendulum is (assuming damping is small) in seconds:
A
0.693b
B
b
C
1b
D
2b
Video Solution
Text Solution
The correct Answer is:D
Refer to figure, The retardation of spherical bob due to viscous force =bυ
∴ Retarding force =mbυ
When angular displacemetn of bob is θ, the net restoring torque on spherical bob about axis of rotation at S is
τ=−mg×AP+mbυ×SP
=mglsinθ+mbυl ...(i)
If α is the angular acceleration of the bob at P and I is the moment of inertia of the spherical bob about axis of rotation at S then
I=ml2
and τ=Iα=ml2α ...(ii)
From (i) and (ii)
ml2α=−mglsinθ+mbυl
or α=−glsinθ+bυl
or d2ldt2=−glsinθ+bυl
or d2θdt2+glsinθ−bυl=0
It is a differential equation of second order, involving sine function. Hence it represents dampled oscillations. For small damping the solumtion of the above differential equaltion will be
θ=θ0e−bt/2sin(ωt+ϕ)
Its angular amplitude at time t=θ0e−bt/2
As per question ,in time t=τ (i.e., average life time ) angular amplitude drops to 1e times its original value θ0
∴θ0e=θ0e−bτ/2 or e−1=e−bτ/2
or 1=bτ/2orτ=2lb
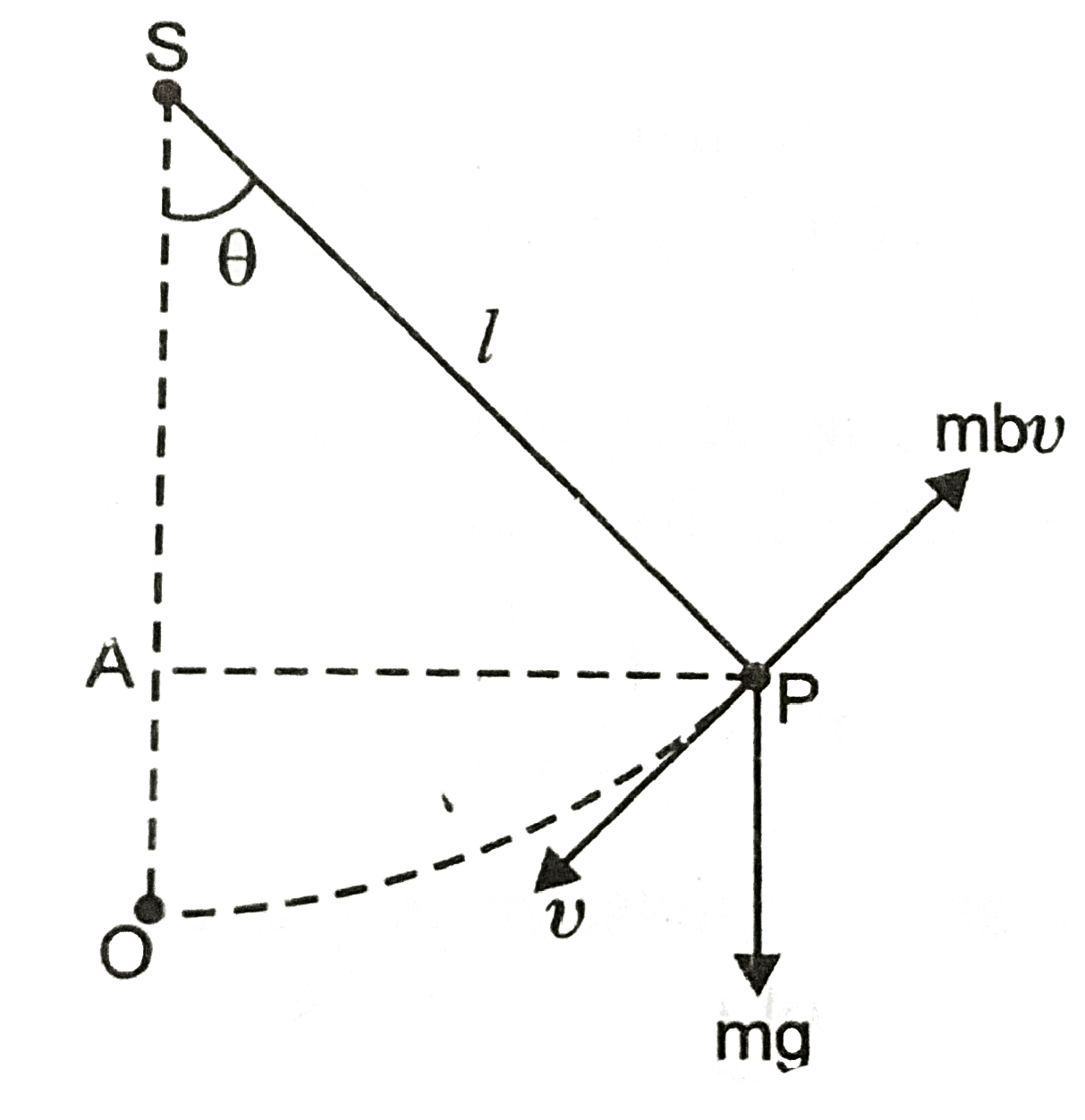
|
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:integer type question
Explore 8 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Assertion-Reason Type Questions
Explore 23 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-II
Explore 14 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
Knowledge Check
The tension in the string of a simple pendulum is maximum, when the bob of the pendulum
Ais at the extreme positionBmidway between the mean position and extreme positionCis at the mean positionDstarts oscillating with very large amplitudesA simple pendulum is set into vibrations. The bob of the pendulum comes to rest after some time due t
AAir frictionBMoment of inertiaCweight of the bobDCombination of all the aboveA simple pendulum has a time period T. If the support and the pendulum fall freely, the time period will be
AinfinityBgreater than TCless than TDzero
A simple pendulum has a time period T. The pendulum is completely immersed in a non-viscous liquid whose density is one-tenth of that of the material of the bob. The time period of the pendulum immersed in liquid is
View SolutionIf the metal bob of a simple pendulum is replaced by a wooden bob, then its time period will
View SolutionIf T and T' are the periods of a simple pendulum and a conical pendulum of the sample length then .
View SolutionThe time period of a simple pendulum is 1.2 s. If the length of the pendulum is doubled, the new time period will be
View SolutionThe time period of a simple pendulum is 1.2 s. If the length of the pendulum is doubled, the new time period will be
View Solution

