When a mass m is connected individually to two spring S1 and S2 , the oscillation frequencies are v1andv2. If the same mass is attached to the two springs as shwon in figure., the oscillation frequecy would be

v1+v2
√v21+v22
(1v1+1v2)−1
√v21−v22
The correct Answer is:B
Let k1 and k2 be the spring constants of springs S1 and s2 respectively. Then
v1=12π√k1mandv2=12π√k2m
If k is the spring constant of two springs S1 and S2 as connected in this problem, the k=k1+k2
If v is the effective frequency of oscillationof the mass attached in this problem, then
v=12π√km=12π√k1+k2m=12π√k1m+k2m=12π√4π2v21+4π2v22=√v21+v22
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-II
Explore 14 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:JEE mains adv..(multiple choice quection)
Explore 150 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:PROBLEMS FOR PRACTICE
Explore 149 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
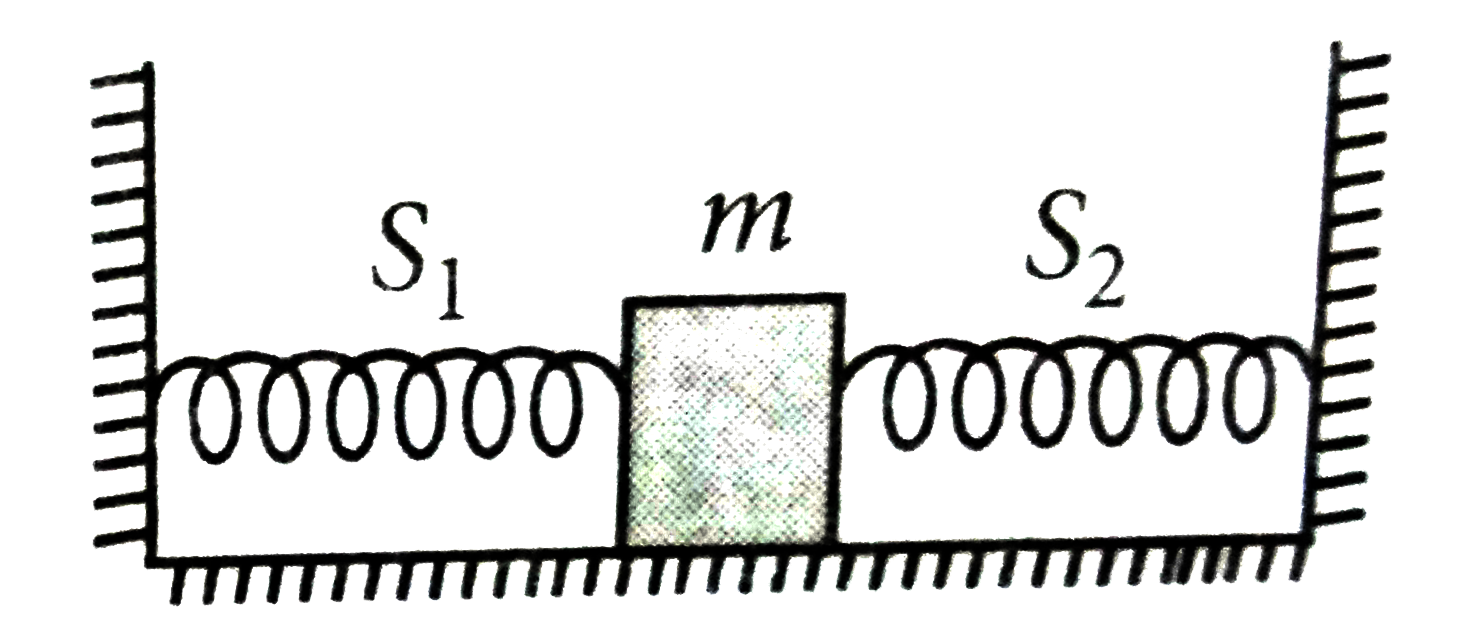
When a mass m is connected individually to two springs S1andS2, the oscillation frequencies are υ1andυ2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
View SolutionA mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is

View Solution
Knowledge Check
When a mass m is connected individually to two springs S1 and S2, the oscillation frequencies are v1 and v2. If the same mass is attached to the two springs as shown in figure, the oscillation frequency would be
 Av1+v2B√v21+v22C(1v1+1v2)−1D√v21−v22
Av1+v2B√v21+v22C(1v1+1v2)−1D√v21−v22Two masses m1 and m2 are attached to a spring balance S as shown in figure. m1>m2 then the reading of spring balance will be .
 .A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
.A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2Two masses m1 and m2 are attached to a spring balance S as shown in Figure. If m1>m2 then the reading of spring balance will be
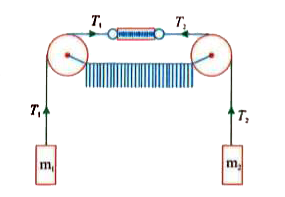 A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
A(m1−m2)B(m1+m2)C2m1m2m1+m2Dm1m2m1+m2
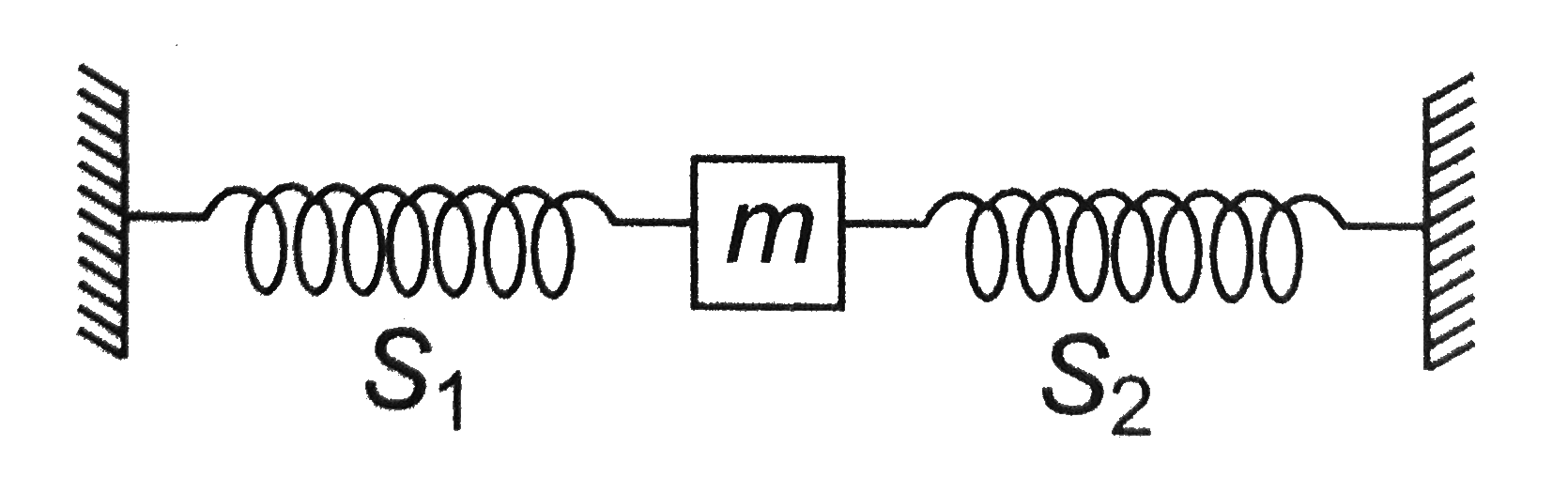
S1andS2 are two identical springs. The oscillation frequency is f. If one springs is removed, frequency will be

View SolutionA particle of mass m is attached to three identical springs of spring constant k as shwon in figure. The time period of vertical oscillation of the particle is

View SolutionIn the figure S1 and S2 are identical springs. The oscillation frequency of the mass m is f. If one spring is removed, the frequency will become

View SolutionIn figure S1 andS1 are identical springs. The oscillation frequency of the mass m is f. if one spring is removed, the frequency will become
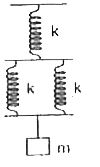
View SolutionCalculate the period of oscillations of block of mass m attached with a set of springs as shown
View Solution

