The vibrations of a string of length 60cm fixed at both ends are represented by the equation----------------------------
y=4sin(πx15)cos(96πt)
Where x and y are in cm and t in seconds.
(i) What is the maximum displacement of a point at x=5cm?
(ii) Where are the nodes located along the string?
(iii) What is the velocity of the particle at x=7.5cm at t=0.25sec.?
(iv) Write down the equations of the component waves whose superpositions gives the above wave.
Compare the given eqn. With standard form of eqn. of stationary wave:
y=2rsin(2πxλ)cos(2πTt)
we find 2r=4,r=2cm,2πλ=π15,λ=30cm.
Hence the string will vibrate in 4 segments, with each segment =λ2=302=15cm as shown in figure,
The nodes are at 0,15cm, 30cm, 45cm and 60cm as shown in figure
(ii) Velocity of particle
υ=dydt=−4sin(πx15)sin96πt×96π
At x=7.5cmandt=0.25s
υ=−4×96πsinπ/2sin(96π×0.25)=Zero
(iii) The component waves of the given stationary wave are
y1=2sin(πx15+96πt), and
y2=2sin(πx15−96πt) 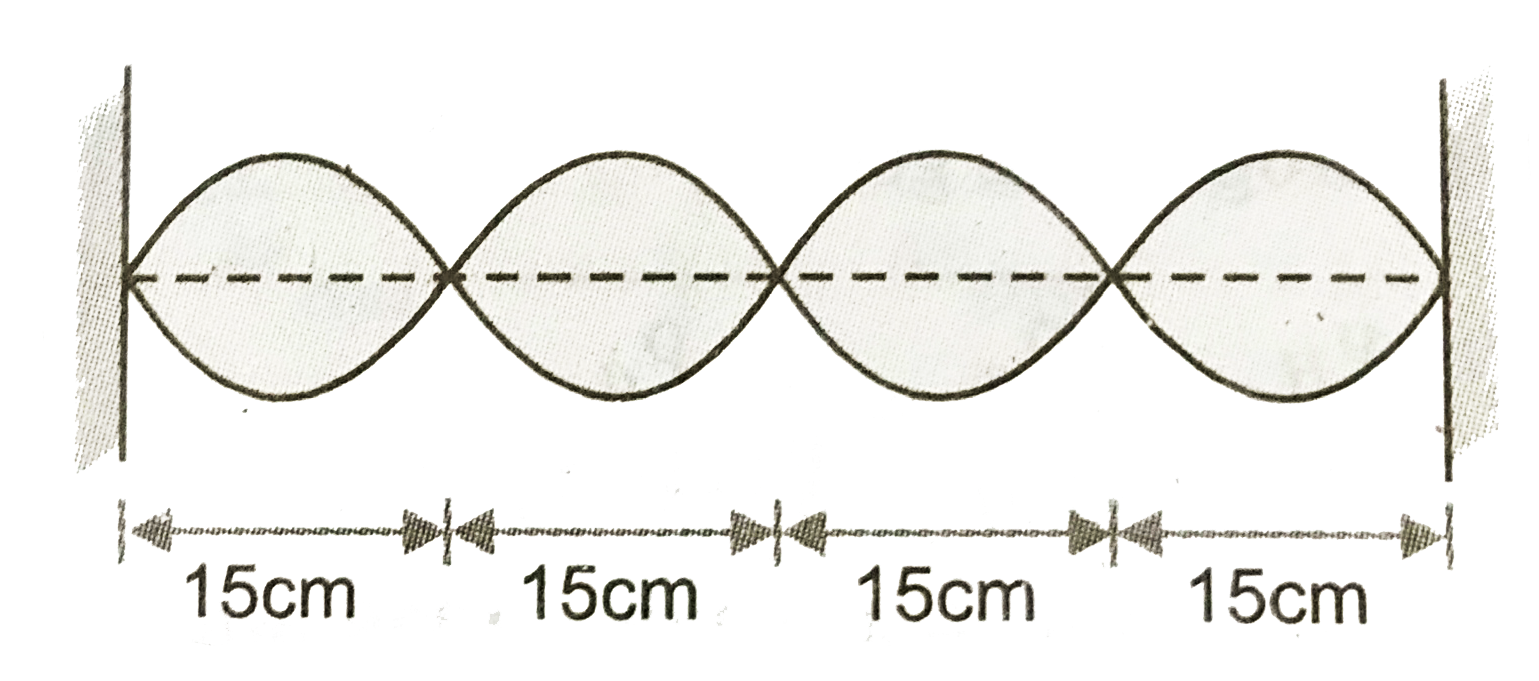
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-I
21 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Multiple Choice Question-II
14 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Fill In The Blanks
20 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
The vibrations of a string of length 60 cm fixed at both ends are represented by the equation y=4sin(πx15)cos(96πt), where x and y are in cm and t in seconds.
(a)What is the maximum displacement of a point at x=5cm?
(b)Where are the nodes located along the string?
(c)What is the velocity of the particle at x=7.5cm and t=0.25s?
(d)Write down the equations of the component waves whose superposition gives the above wave.
View SolutionThe vibrations of a string of length 60cm fixed at both cnds are represented by the equation.
y=4sin(πx/(15))cos(96πt), where x and y are in cm and t in second. The maximum displacement (in cm ) at x= 52 (cm) is
View Solution
Knowledge Check
The vibrations of a string of length 600cm fixed at both ends are represented by the equation y=4sin(πx15)cos(96πt)
where x and y are in cm and t in seconds.AThe maximum displacement of a particle at x=5cm is 2√3cm.BThe nodes located along the string are 15n where ineger n varies from 0 to 40.CThe velocity of the particle at x=7.5cm at t=0.25sec is zeroDThe equations of the component waves whose superpostion gives the above wave are 2sin2π(x30+48t),2sin2π(x30−48t)The vibrations of a string of length 60 cm fixed at both ends are represented by the equation
y=4sin(πx/15)cos(96πt)
where x and y are in cm and t in seconds. The maximum displacement at x = 5 cm is–A2√3cmB3√2cmC√2cmD√3cmThe vibrations of string of length 60cm fixed at both ends are presented by the equations
y=4sin(πx/15)cos(96πt)
where xandy are in cm and t in s. The maximum displacement at x=5cm isA2√3cmB4cmCzeroD4√2cm
The vibrations of a string of length 60 cm fixed at both the ends are represented by the equation y=2sin(4πx15)cos(96πt) where x and y are in cm. The maximum number of loops that can be formed in it is
View SolutionThe vibrations of a string of length 60cm fixed at both ends are represented by the equation
y=4sin(πx15)cos(96πt)
where x and y are in cm and t in second .
ii. Where are the nodes located along the strings ?
iii. What is the velocity of the particle at x=7.5cmatt=0.25s?
iv. Write down the equations of component waves whose superposition gives the above waves .
View SolutionThe vibration of a string of length 60cm is represented by the equation,
y=3cos(πx/20)cos(72πt) where x & y are in cm and t in sec.
(i) Write down the compoent waves whose superposition gives the above wave.
(ii) Where are the nodes and antinodes located along the string.
(iii) What is the velocity of the particle of the string at the position x=5cm & t=0.25 sec.
View SolutionThe vibration of a string of length 60cm fixed at both ends are represented by displacedment y=4sin(πx15)cos(96π)wherexandyare∈cmandt∈second.Thepartic≤velocityatx=22.5 and t=0.25 is
View SolutionThe vibrations of a string fixed at both ends are represented by y=16sin(πx15)cos(96πt). Where 'x' and 'y' are in cm and 't' in seconds. Then the phase difference between the points at x=13cm and x=16 in radian is
View Solution