In the third normal mode of vibrationn of a closed organ pipe, the number of nodes and antinodes respectively are
4,3
3,4
3,3
4,4
The correct Answer is:C
To solve the problem of determining the number of nodes and antinodes in the third normal mode of vibration of a closed organ pipe, we can follow these steps:
Step 1: Understand the structure of a closed organ pipe
A closed organ pipe has one end closed (node) and the other end open (antinode). The closed end will always have a node, where the displacement of air is zero, while the open end will have an antinode, where the displacement is maximum.
Hint: Remember that closed ends have nodes and open ends have antinodes.
Step 2: Identify the normal modes of vibration
In a closed organ pipe, the normal modes of vibration can be represented as follows:
- The first normal mode (fundamental frequency) has 1 node (at the closed end) and 1 antinode (at the open end).
- The second normal mode has 2 nodes and 1 antinode.
- The third normal mode has 3 nodes and 2 antinodes.
Hint: Each successive normal mode adds one additional node and one additional antinode.
Step 3: Analyze the third normal mode
In the third normal mode of vibration:
- The closed end still has 1 node.
- There will be additional nodes along the length of the pipe. For the third mode, we will have a total of 3 nodes.
- The open end will have 1 antinode, and there will be additional antinodes in between. For the third mode, we will have a total of 3 antinodes.
Hint: Count the nodes and antinodes carefully in the diagram of the third normal mode.
Step 4: Conclusion
From the analysis, we conclude that in the third normal mode of vibration of a closed organ pipe, there are:
- Number of nodes: 3
- Number of antinodes: 2
Thus, the answer is:
- Nodes: 3
- Antinodes: 2
Final Answer
The number of nodes and antinodes in the third normal mode of vibration of a closed organ pipe are 3 and 2, respectively.
---
A closed organ pipe has one end closed (node) and the other end open (antinode). The closed end will always have a node, where the displacement of air is zero, while the open end will have an antinode, where the displacement is maximum.
In a closed organ pipe, the normal modes of vibration can be represented as follows:
- The first normal mode (fundamental frequency) has 1 node (at the closed end) and 1 antinode (at the open end).
- The second normal mode has 2 nodes and 1 antinode.
- The third normal mode has 3 nodes and 2 antinodes.
In the third normal mode of vibration:
- The closed end still has 1 node.
- There will be additional nodes along the length of the pipe. For the third mode, we will have a total of 3 nodes.
- The open end will have 1 antinode, and there will be additional antinodes in between. For the third mode, we will have a total of 3 antinodes.
From the analysis, we conclude that in the third normal mode of vibration of a closed organ pipe, there are:
- Number of nodes: 3
- Number of antinodes: 2
- Nodes: 3
- Antinodes: 2
The number of nodes and antinodes in the third normal mode of vibration of a closed organ pipe are 3 and 2, respectively.
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Fill In The Blanks
Explore 20 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:PROBLEMS FOR PRACTICE
Explore 149 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Value Based Questions
Explore 5 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
Knowledge Check
In closed organ pipe at one end-
 AA-T,B-P,C-P,D-TBA-S,B-P,C-P,D-(Q,T)CA-S,B_Q,C-R,D-QDA-R,B_Q,C-S,D-(Q,T)
AA-T,B-P,C-P,D-TBA-S,B-P,C-P,D-(Q,T)CA-S,B_Q,C-R,D-QDA-R,B_Q,C-S,D-(Q,T)Modes of vibration in a closed organ pipe are represented by –
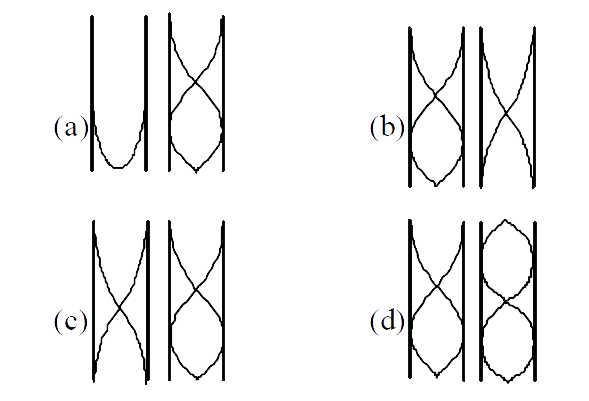 AaBbCcDd
AaBbCcDdIn the fundamental mode of vibration on a stretched string, the number of antinodes are
AOneBTwoCThreeDNone
Assertion : In the nth normal mode of vibration of a string, there are (n+1) nodes and n antinodes.
Reason : This is because both the ends of the string are fixed and from nodes.
View SolutionIn the 5th overtone of an open organ pipe, these are (N-stands for nodes and A- for antinodes)
View SolutionModes of vibration in an open organ pipe are represented by –
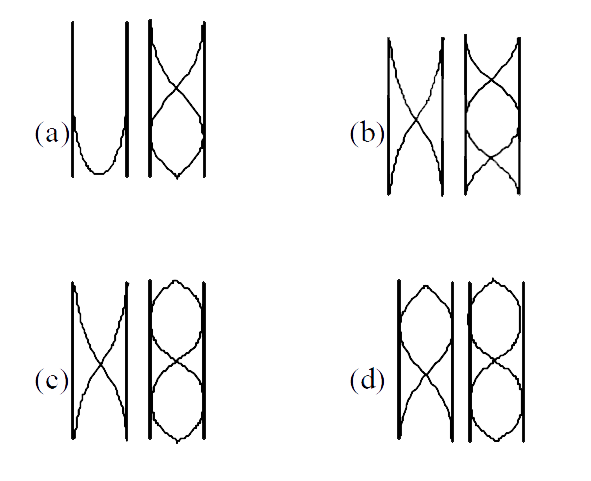
View SolutionA closed organ pipe emits harmonics in the ratio of
View SolutionA tuning fork vibrats with frequnecy 256Hz and gives one beat per seond with the third normal mode of vibration of an open pipe. What is the length of the pipe (Speed of sound in air is 340ms−1)
View Solution


