A mass attached to a spring is free to oscillate, with angular velocity $ω$ , in a horizontal plane without friction or damping. It is pulled to a distance $x_{0}$ and pushed towards the centre with a velocity $v_{0}$ at time $t = 0$ . Determine the amplitude of the resulting oscillations in terms of the parameters $o m η, x_{0} and v_{0}$ .

Video Solution

Text Solution

Verified by Experts

When $t = 0, x = x_{0}$ and $\frac{d x}{d t} = - v_{0}$ $∴$ From $x = A cos (ω t + θ), x_{0} = A cos θ$ …(i)
velocity $\frac{d x}{d t} = - A ω sin (ω t + θ)$
$- v_{0} = - A ω sin θ or A sin θ = v_{0} / ω$ …(ii)
Squaring and adding (i) and (ii), we get
$A^{2} ({sin}^{2} θ + {cos}^{2} θ) = (v_{0}^{2} / ω^{2}) + x_{0}^{2}$
$A = {[v_{0}^{2} / ω^{2} + x_{0}^{2}]}^{1 / 2}$

Updated on:21/07/2023

A mass attached to a string rotates about a fixed centre with an angular velocity $ω$ in a horizontal plane ,The length of the string and the angular velocity are now doubled .IF $T_{0}$ is the initial tension in the string , then the new tension will be
A $2 T_{0}$
B $4 T_{0}$
C $8 T_{0}$
D $6 T_{0}$
A block of mass $m$ is pushed towards the movable wedge of mass $M$ and height $h$ , with a velocity $v_{0}$ . All surfaces are smooth . The minimum value of $v_{0}$ for which the block will reach the top of the wedge is

A $\sqrt{2 g h}$
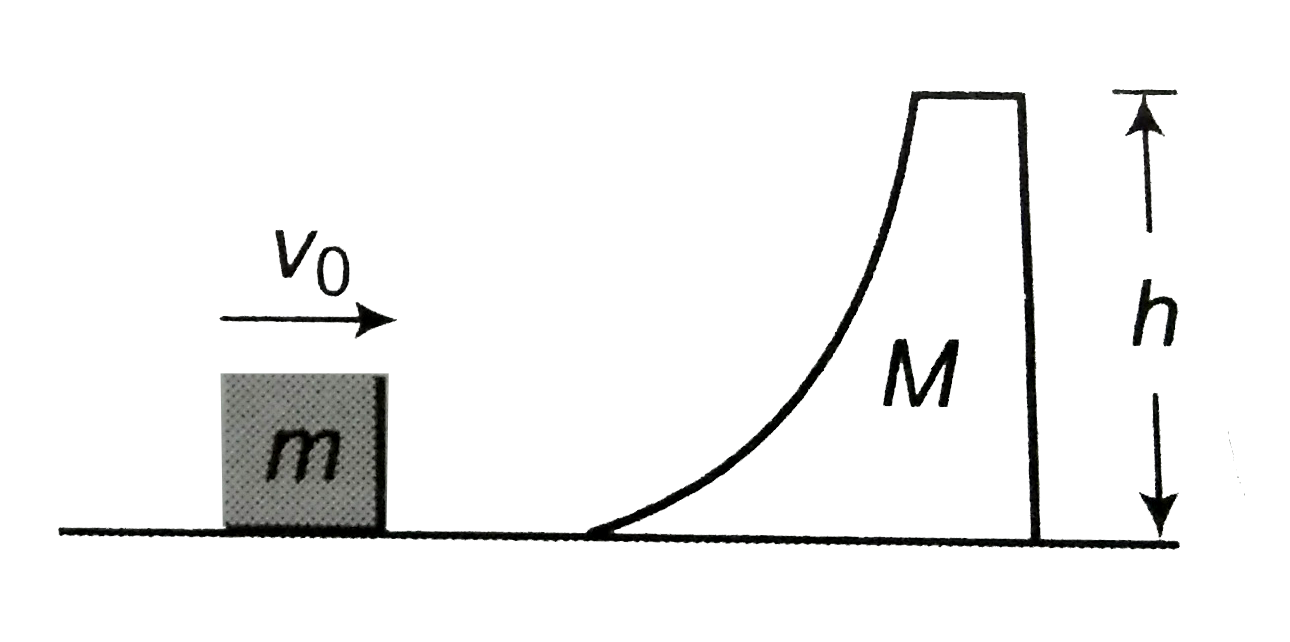B $\sqrt{\frac{2 g h m}{M}}$
C $\sqrt{\frac{2 g h (m + M)}{M}}$
D $\sqrt{\frac{2 g h m}{(m + M)}}$
A uniform ring of radius $R$ is given a back spin of angular velocity $V_{0} / 2 R$ and thrown on a horizontal rough surface with velocity of centre to be $V_{0}$ . The velocity of the centre of the ring when it starts pure rolling will be
A $\frac{V_{0}}{2}$
B $\frac{V_{0}}{4}$
C $\frac{3 V_{0}}{4}$
D $0$