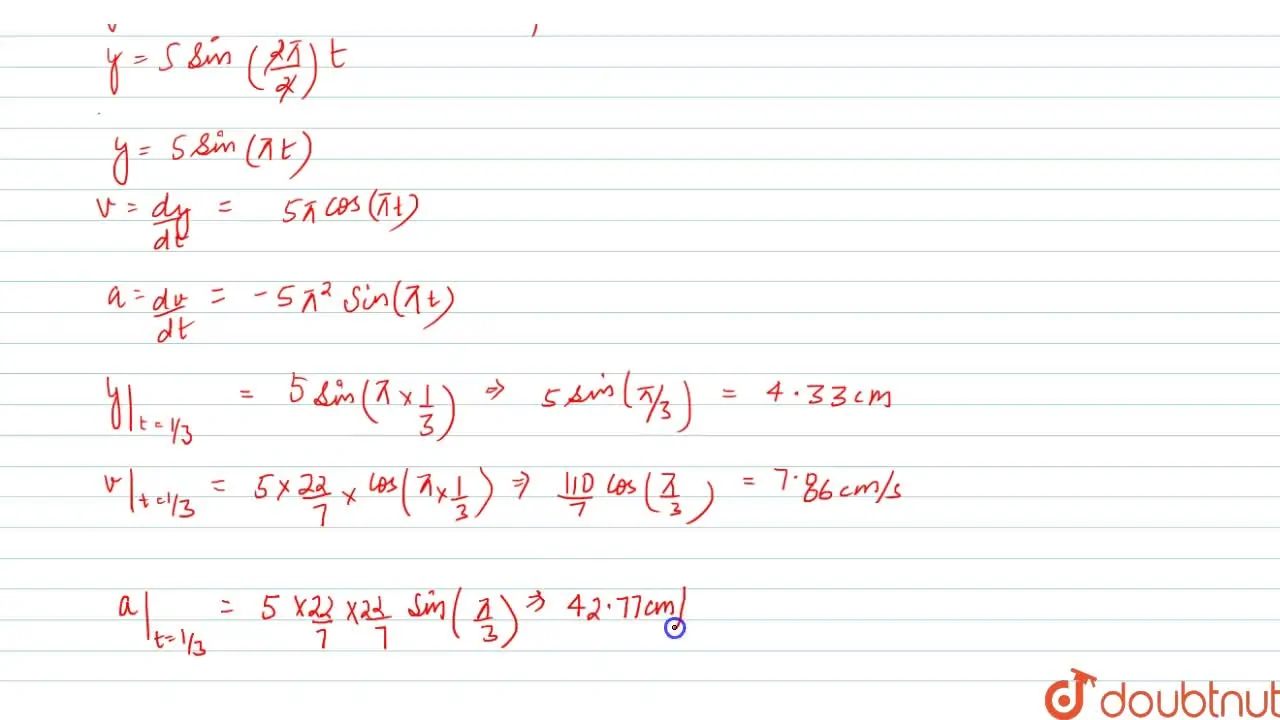A particle executes SHM with a time period of 2s and amplitude 5 cm. Find (i) displacement (ii) velocity (iii) acceleration, after 1/3 second, starting from mean position.
Here, T=2s,a=5cm,t=13s.
(a) Displacement , y=asin(2πT)t=5sin(2π2)×13=5×(√32)=4.33cm
(b) Velocity , V=dydt=a2πTcos(2πT)t=5×2π2xos(2π2)×13=7.86cm/s
(c) Acceleration, A=dVdt=−4pπr2T2asin(2πT)t=4×π24×5×sin(2π2)×13
=44×(227)2×5×√32=−42.77cm/s2
Related Playlists
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - CURIOSITY QUESTION2videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - SOLVED EXAMPLES54videos
OSCILLATIONS AND WAVES
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
- BOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance18videos
PHYSICAL WORLD AND MEASUREMENT
Similar Questions
A particle executed SHM iwht a time period of 3s and amplitude 6cm. Find (i) displacement (ii) velocity and (iii) acceleration, after 1/2 second, starting from the mean position.
View SolutionA particle executes SHM with a time period of 2s and amplitude 10 cm . Find its (i) Displacement (ii) Velocity (iii) Acceleration after 1/6 s, Starting from mean position.
View SolutionA particle executes SHM with a time period of 2 s and amplitude 5 cm. What will be the displacement and velocity of that particle at t = 1/3 ?
View SolutionA particle is executing simple harmonic motion with time period of 4 s and amplitude 10 cm. Calculate displacement, velocity after 12 second starting from mean position.
View SolutionA particle is executing simple harmonic motion with a time period of 2s and amplitude 10 cm. Calculate its velocity and acceleration 2 seconds after starting from mean position.
View SolutionA particle executes S.H.M. with a period of 6 second and amplitude of 3 cm . Its maximum speed in cm / sec is
View SolutionA particle is executing simple harmonic motion with an amplitude of 10 cm and time period of 4s. Calculate its displacement, velocity and acceleration after 1/2 seconds, starting from the mean position.
View SolutionA particle executing SHM with time period T and amplitude A. The mean velocity of the particle averaged over quarter oscillation, is
View SolutionIf a particle executes SHM of time period 4 s and amplitude 2 cm, find its maximum velocity and that at half its full displacement also find the acceleration at the turning points and when the displacement is 0.75 cm
View SolutionA particle executes S.H.M. of amplitude A . At what positions of its displacement (x), will its acceleration be zero and maximum ?
View Solution