Two wires of equal length and cross sectional area suspended as shown in
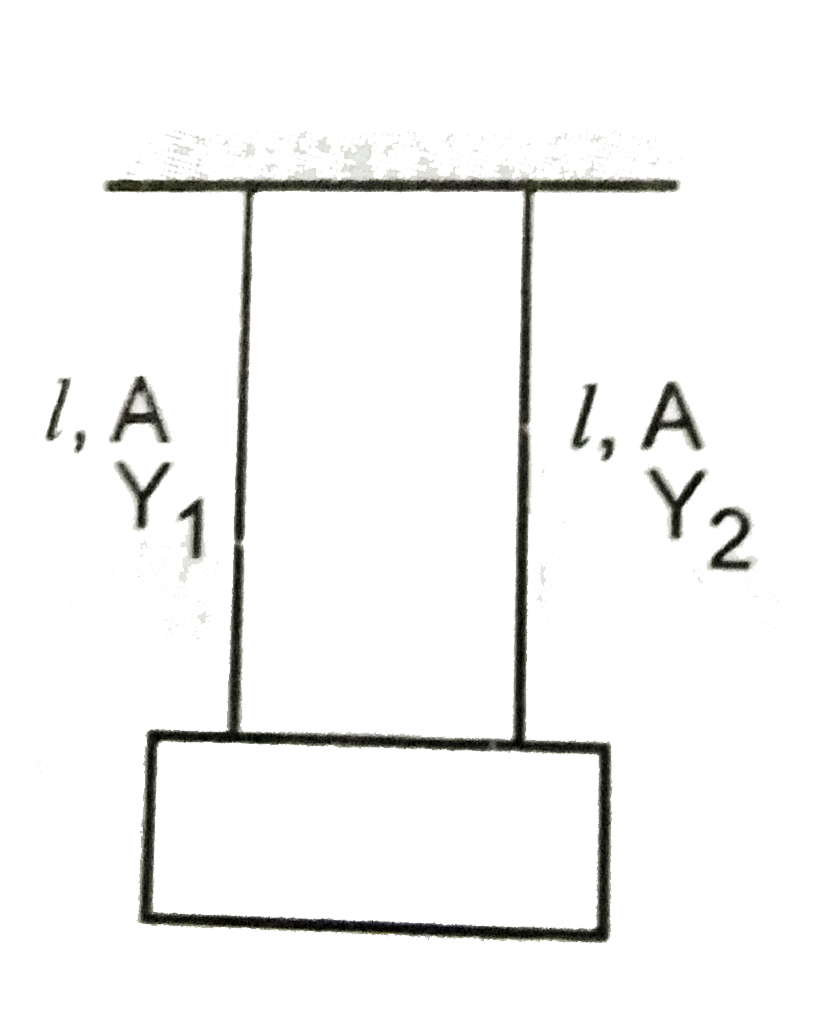
Their Young's modulii are Y1=2×1011 Pa and Y2=0.90×1011 Pa respectively. What will be the equivalent Young's modulus of combination?
2.90×1011 Pa
1.45×1011 Pa
1.34×1011 Pa
None of this above
The correct Answer is:B
The spring constant of a wire is given by
k=FΔl=YAl
the equivalent spring constant of a wire is given by
Keq−k1+k2
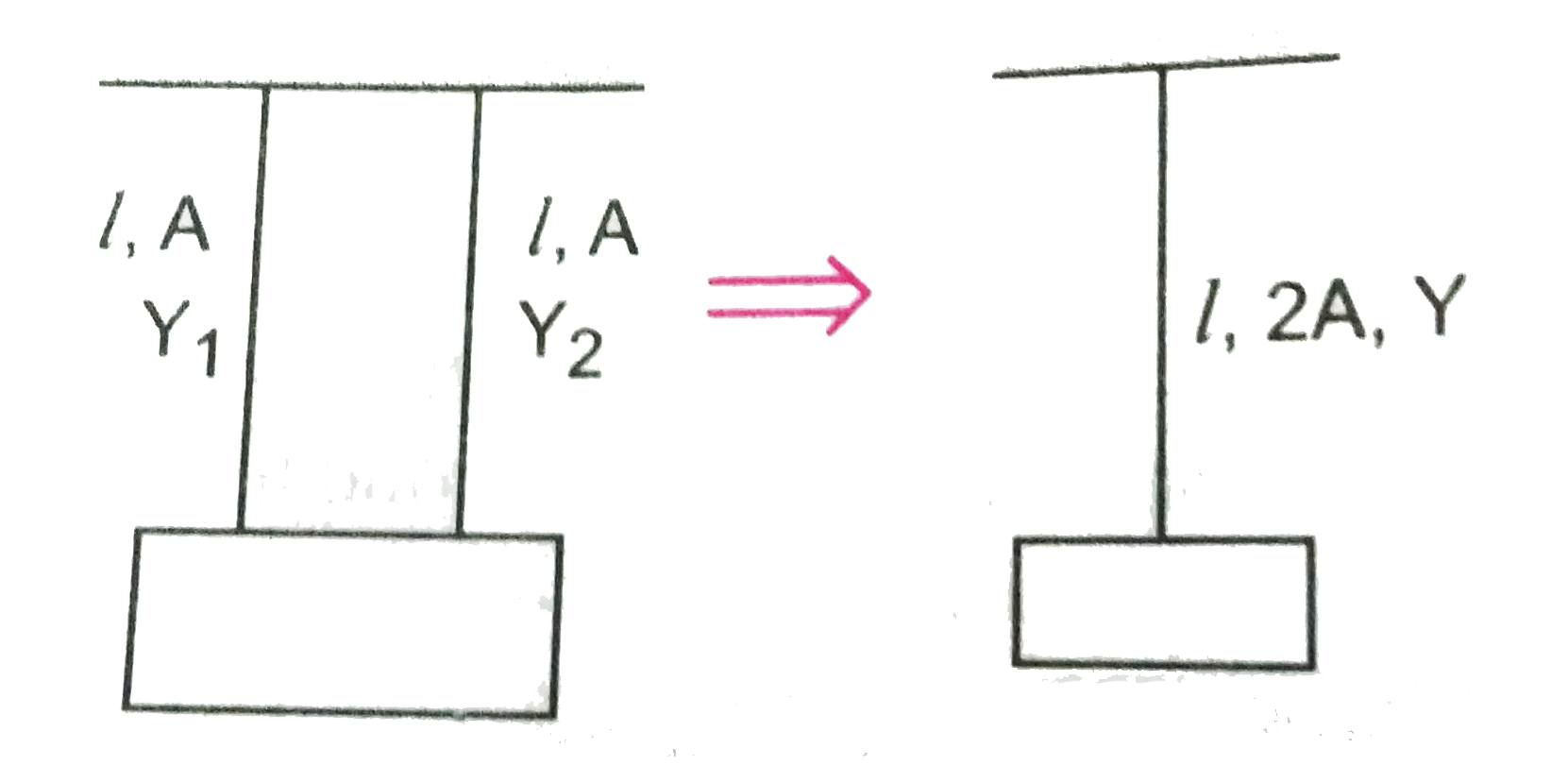
or Y2Al=Y1Al+Y2Al
or Y=Y1+Y22=2×1011+0.9×10112
=1.45×1011 Pa
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
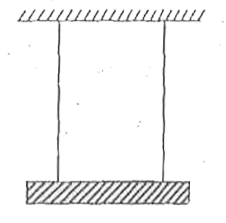
Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View Solution
Knowledge Check
Two wires of equal length and cross-section area suspended as shown in figure. Their Young's modulus are Y1 and Y2 respectively. The equavalent Young's modulus will be
 AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1−Y22CY1Y2Y1+Y2D√Y1Y2Two wires of equal length and cross-sectional area are suspended as shown in figure. Their Young's modullare Y1 andY2 respectively. The equivalent Young's modulil will bebr>
 AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2
AY1+Y2BY1+Y22CY1Y2Y1+Y2D√Y1Y2Two wires of equal dimensions and young's modulus Y1 and Y2 are connected end to end. What is the equivalent young's modulus for the combination?
AY1+Y22B√Y1+Y2C2Y1Y2Y1+Y2D√Y21y222
A horizontal rod suspended from two wires of same length and cross - section. Their Young's modulus are Y1 and Y2 respectively. The equivalent Young's modulus will be

View SolutionThe elastic limit and ultimate strength for steel is 2.48×108Pa and 4.89×108Pa respectively. A steel wire of 10 m length and 2 mm cross sectional diameter is subjected to longitudinal tensile stress. Young’s modulus of steel is Y=2×1011Pa
(a) Calculate the maximum elongation that can be produced in the wire without permanently deforming it. How much force is needed to produce this extension?
(b) Calculate the maximum stretching force that can be applied without breaking the wire.
View SolutionTwo wires of diameter 0.25cm, one made of steel and other made of brass, are loaded as shown in the figure. The unloaded length of the steel wire is 1.5m and that of brass is 1.0m. Young's modulus of steel is 2.0×1011Pa and that of brass is 1.0×1011 Pa. Compute the ratio of elongations of steel and brass wires. △lsteel△lbrass=?

View SolutionThe force required to stretch a steel wire 1cm2 in cross - section to increase its length by 1%,if its Young's modulus is 2×1011Nm−2,is
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
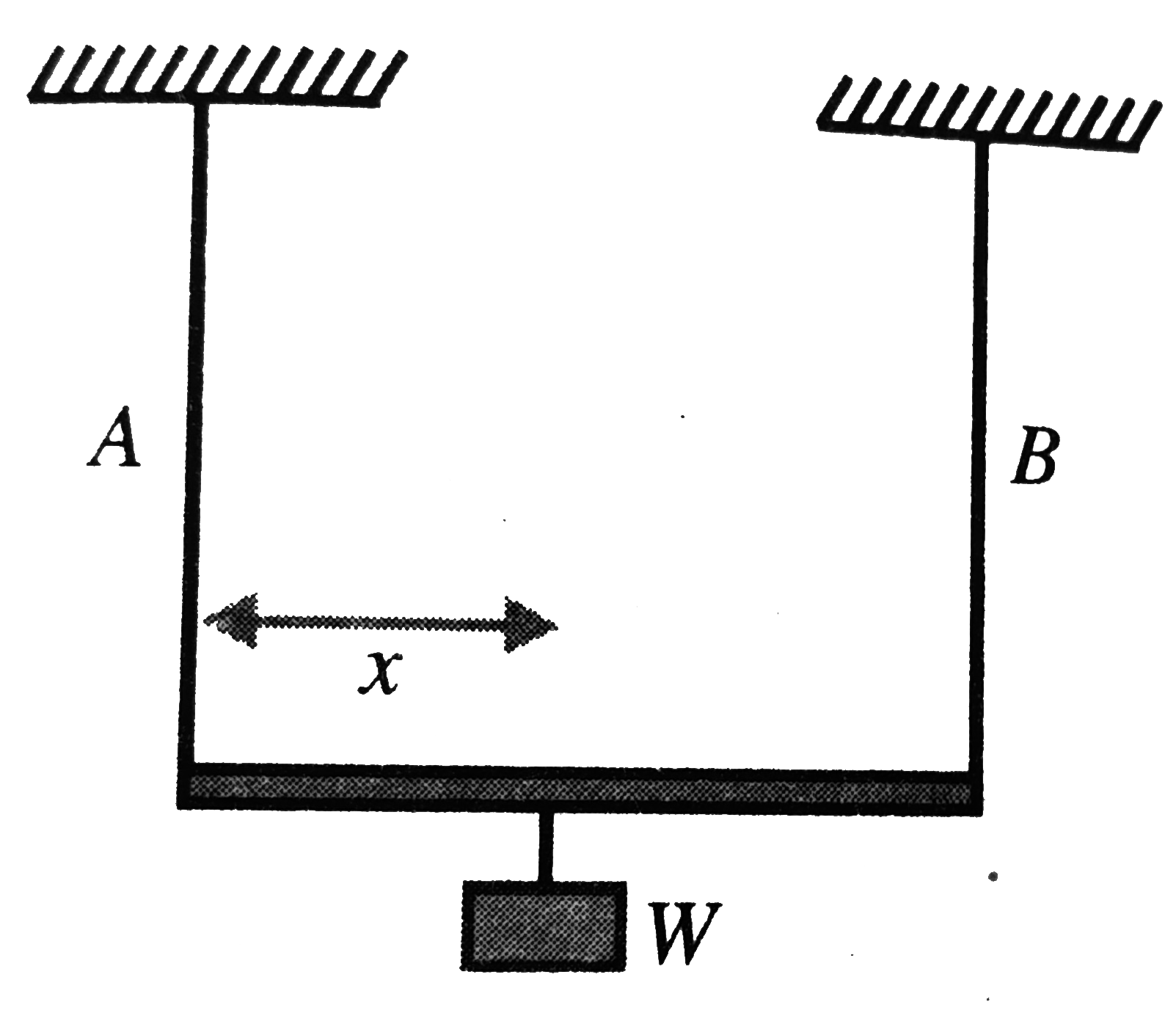
Determine the value of x so that equal strains are produced in each wire
View Solution
