Two wires of equal cross section but one made of steel and the other of copper, are joined end to end. When the combination is kept under tension, the elongations in the two wires are found to be equal. Find the ratio of the lengths of the two wires. Young modulus of steel and that of copper
The correct Answer is:20//11
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions-II
Explore 14 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions-I
Explore 173 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Fill in the Blanks E
Explore 10 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
A steel wire and a copper wire of equal length and equal cross sectionasl area area joined end to end and the combination is subjected to as tension. Find the ratio of as. The stresses developed in the two wire and b. the strains developed. Y of steel =2×1011Nm−2. Y o copper =1.3×1011Nm−2.
View SolutionCompute the elongation of the steel wire in the figure. Unloaded length of the steel wire =1.5 m, the diameter of the wire is 0.25 m, Young's modulus of steel is 2×1011 N m−2.
View Solution
Knowledge Check
Two wires of equal cross-section but one made of steel and the other of copper are joined end to end. When the cobination is kept under tension, the elongations in the two wires are found to be equal elongations in the two wire are found to be equal. What is the ratio of the lengths of the two wires?
(Given, Young's modulus of steel =2×1011Nm−2 and young's modulus of copper =1.1×1011Nm−2)A2:11B11:2C20:11D11:20A light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]
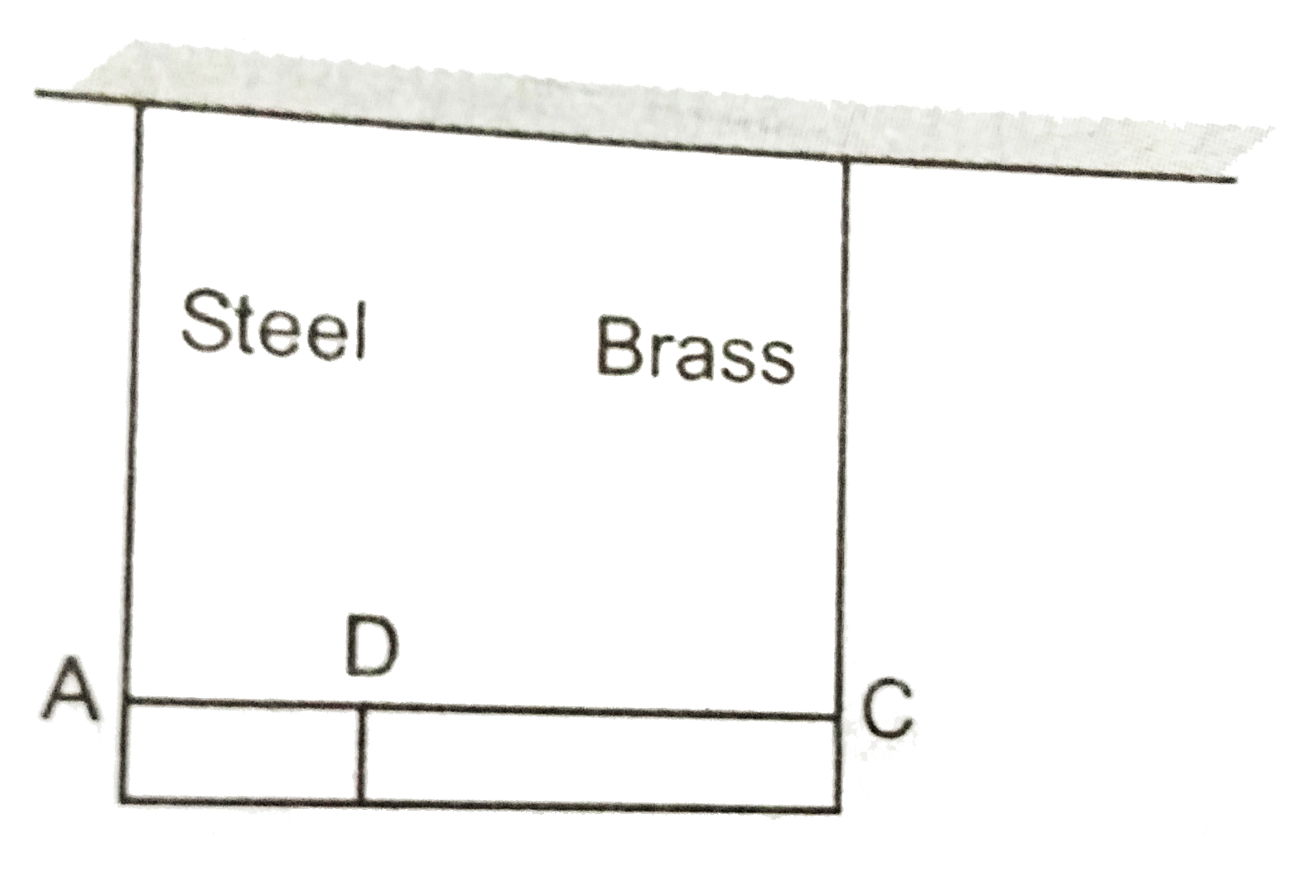 A1.00mB(2/3)mC(4/3)mD(5/3)m
A1.00mB(2/3)mC(4/3)mD(5/3)mTwo wire of same radius and lengh the are subjected to the same load. One wire is of steel and the other is of copper. If the Young's modulus of steel is twice that of copper, the ratio the energy stored per unit volume in steel to that of copper wire is
A1:2B2:1C1:4D4:1
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
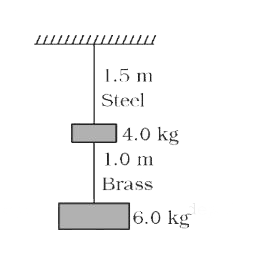
View SolutionOne end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceilign and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View SolutionIn figure the upper wire is made of steel and the lower of copper. The wires have equal cross section. Find the ratio of the longitudinals strains developed in the two wires.

View SolutionA steel wire and a copper wire of equal length and equal cross- sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of
copper/steel
(a) the stresses developed . In the two wires,
(b) the strains developed. (Y of steel =2×1011N/m2)
View SolutionA Copper wire of length 2.2m and a steel wire of length 1.6m, both of diameter 3.0mm are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied . Young's modulus of copper is 1.1×1011Nm−2 and Young's modulus of steel is 2.0×1011Nm−2.
View Solution

