A man, the surface area of whose skin is 2m2 , is sitting in a room where air temperature is 20∘C if his skin temperature is 28∘C and emissivity of his skin equals 0.97, find the rate at which his body loses heat.
To find the rate at which the man's body loses heat, we can use the Stefan-Boltzmann law, which is given by the formula:
P=ϵ⋅A⋅σ⋅(T4−T40)
Where:
- P is the power (rate of heat loss) in watts (W),
- ϵ is the emissivity of the skin,
- A is the surface area of the skin,
- σ is the Stefan-Boltzmann constant, approximately 5.67×10−8W/m2K4,
- T is the absolute temperature of the skin in Kelvin,
- T0 is the absolute temperature of the surrounding air in Kelvin.
Step 1: Convert temperatures from Celsius to Kelvin
- The surrounding air temperature is 20∘C:
T0=20+273=293K
- The skin temperature is 28∘C:
T=28+273=301K
Step 2: Substitute the known values into the formula
- Given:
- Surface area A=2m2
- Emissivity ϵ=0.97
- Stefan-Boltzmann constant σ=5.67×10−8W/m2K4
Now, substituting these values into the formula:
P=0.97⋅2⋅5.67×10−8⋅(3014−2934)
Step 3: Calculate T4 and T40
- Calculate 3014:
3014=8.267×109
- Calculate 2934:
2934=7.688×109
Step 4: Find the difference T4−T40
3014−2934=8.267×109−7.688×109=0.579×109=5.79×108
Step 5: Substitute back into the power equation
P=0.97⋅2⋅5.67×10−8⋅5.79×108
Step 6: Calculate P
P=0.97⋅2⋅5.67⋅5.79≈0.97⋅2⋅32.88≈63.96W
Step 7: Final Calculation
After calculating the exact values:
P≈92.2W
Conclusion
The rate at which the man's body loses heat is approximately 92.2W.
- P is the power (rate of heat loss) in watts (W),
- ϵ is the emissivity of the skin,
- A is the surface area of the skin,
- σ is the Stefan-Boltzmann constant, approximately 5.67×10−8W/m2K4,
- T is the absolute temperature of the skin in Kelvin,
- T0 is the absolute temperature of the surrounding air in Kelvin.
- The surrounding air temperature is 20∘C:
T0=20+273=293K
- The skin temperature is 28∘C:
T=28+273=301K
- Given:
- Surface area A=2m2
- Emissivity ϵ=0.97
- Stefan-Boltzmann constant σ=5.67×10−8W/m2K4
P=0.97⋅2⋅5.67×10−8⋅(3014−2934)
- Calculate 3014:
3014=8.267×109
- Calculate 2934:
2934=7.688×109
3014−2934=8.267×109−7.688×109=0.579×109=5.79×108
P=0.97⋅2⋅5.67×10−8⋅5.79×108
P=0.97⋅2⋅5.67⋅5.79≈0.97⋅2⋅32.88≈63.96W
After calculating the exact values:
P≈92.2W
The rate at which the man's body loses heat is approximately 92.2W.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Conceptual Problems
Explore 103 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Advanced problems for competitions
Explore 21 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Long Answer questions
Explore 33 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
A spherical ball of surface area 2×10−3m2 is suspended in a room at temperature 330 K. If the temperature of the ball is 200∘C, find the net rate of loss of heat from the ball if it behaves like a black body.
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
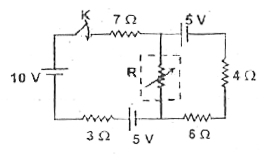
View Solution
Knowledge Check
Calculate radiationn powe for sphere whose temperature is 227∘C and radius 2 m and emissivity 0.8.
A1425 WB1500WC1255WD1575WA scientist says that the efficiency of his heat engine which operates at source temperature 127∘C and sink temperature 27∘C is 26%, then
AIt is impossibleBIt is possible but less probableCIt is quite probableDData are incompleteA body radiates heat at the rate of 5 cal/m2−s when its temperature is 227∘C. The heat radiated by the body when its temperature is 727∘C is
A10 calm2 sB20 cal/m2 sC40 cal/m2 sD80 cal/m2 s
A blackbody of sarface area 10cm2isheated→127^(@)Candissuspended∈ar∞mattemperature27^(@)C calculate the initial rate of loss of heat from the body to the room.
View Solution(a) Calculate the rate at which body heat is conducted through the clothing of a skier in a steady-state process, given the following data: the body surface area is 1.8m2, and the clothing is 1.0 cm thick , the skin surface temperature is 33∘C and the outer surface of the clothing is at 1.0∘C, the thermal conductivity of the clothing is 0.040W/m.K. (b) If , after a fall, the skier's clothes became soaked with water of thermal conductivity 0.60W/m.K, by how much is the rate of conduction multiplied ?
View SolutionWater is filled in a vessel which is kept in a room at a temperature of 20∘C. The temperature of the water is slowly increased. When the temperature of water is 40∘C, it loses heat at the rate of 10cal/s. What will be the rate of loss of heat when the temperature of water is 80∘C ?
View SolutionA scientist says that the efficiency of his heat engine which operates at source temperature 127∘C and sink temperature 27∘Cis26%, then
View SolutionAn object is being heated by a heater supplying 60W of heat. Temperature of surrounding is 20∘C and the temperature of object becomes constant at 50∘C Now the heater is switched off What is the rate at which the object will lose heat when its temperature has dropped to 30∘C .
View Solution