Rain drops falling under gravity do not acquire very high velocity. Why?

Video Solution

Text Solution

Generated By DoubtnutGPT

To understand why raindrops falling under gravity do not acquire very high velocity, we need to analyze the forces acting on them.
1. Understanding the Forces Acting on Raindrops:
When a raindrop falls, two main forces act on it: the gravitational force (weight) pulling it downward and the viscous drag force opposing its motion.
- Gravitational Force (Weight): This force can be expressed as $F_{g} = m g$ , where $m$ is the mass of the raindrop and $g$ is the acceleration due to gravity.
- Viscous Drag Force: As the raindrop moves through the air, it experiences a drag force due to the viscosity of the air. This force opposes the motion of the raindrop.
2. Applying Newton's Second Law:
According to Newton's second law, the net force acting on the raindrop is equal to the mass of the raindrop multiplied by its acceleration:
$F_{n e t} = m a$
Here, the net force can be expressed as:
$F_{n e t} = F_{g} - F_{d}$
where $F_{d}$ is the viscous drag force.
3. Terminal Velocity Concept:
As the raindrop accelerates downward, its speed increases, and consequently, the viscous drag force also increases. Eventually, the drag force becomes equal to the gravitational force:
$F_{d} = F_{g}$
At this point, the net force becomes zero, and the raindrop stops accelerating. It then continues to fall at a constant speed known as the terminal velocity ( $V_{t}$ ).
4. Factors Affecting Terminal Velocity:
The terminal velocity is not very high for raindrops due to the following reasons:
- The size of the raindrop: Smaller raindrops have a lower terminal velocity because the viscous drag force increases with the surface area.
- The density of the air: The denser the medium, the greater the drag force acting on the raindrop.
5. Conclusion:
Therefore, raindrops do not acquire very high velocities when falling under gravity because the viscous drag force counteracts the gravitational force, leading to a constant terminal velocity that is relatively low.

Updated on:7/8/2024

Rain drops fall with terminal velocity due to
Abuoyancy
Bviscosity
Clow weight
Dsurface tension
Rain drops fall from a great height under gravity. Check the correct statement
ATheir velocity continuously increases till they hit the earth will the same final velocity.
BThey fall with a terminal velocity which is different for drops of different sizes.
CThey fall with a terminal velocity which is the same for very drop.
DTheir velocity goes on increasing continuously till they hit the earth, and the final velocity of each drop is different.
At t = 0 source starts falling under gravity and a detector is projected upwards with a velocity 10m/s. For the vertical upward motion of detector

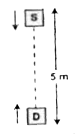Aapparent frequency received by detector = source frequency.
Binitially apparent frequency $>$ source frequency and finally less than source frequency.
Capparent frequency depends only on the detector velocity.
Ddate insufficient.