To lift an automobile of 2000 kg, a hydraulic pump with a large piston 30 cm square in area is employed. Calculate the force that must be applied to pump a small piston of area 10 square cm to achieve it.
To solve the problem of lifting an automobile using a hydraulic pump, we can apply Pascal's principle, which states that pressure applied to a confined fluid is transmitted undiminished in all directions throughout the fluid.
1. Identify the Given Data:
- Mass of the automobile (m) = 2000 kg
- Area of the large piston (A1) = 30 cm² = 30 × 10⁻⁴ m² = 0.003 m² (conversion to m²)
- Area of the small piston (A2) = 10 cm² = 10 × 10⁻⁴ m² = 0.001 m² (conversion to m²)
2. Calculate the Weight of the Automobile:
- Weight (W) = mass × gravitational acceleration (g)
- Here, g = 9.81 m/s² (approximate value)
- W = 2000 kg × 9.81 m/s² = 19620 N
3. Apply Pascal's Principle:
- According to Pascal's principle, the pressure applied on the small piston is equal to the pressure exerted by the large piston.
- Pressure (P) = Force (F) / Area (A)
- For the large piston:
P1=F1A1
- For the small piston:
P2=F2A2
- Since P1=P2, we can write:
F1A1=F2A2
4. Substitute Known Values:
- We know F1=W=19620N, A1=0.003m², and A2=0.001m².
- Substitute these values into the equation:
19620N0.003m²=F20.001m²
5. Solve for F2:
- Rearranging gives:
F2=19620N×0.001m²0.003m²
- Calculate F2:
F2=19620×0.0010.003=196203=6540N
6. Final Calculation:
- The force that must be applied to the small piston to lift the automobile is F2=6540N.
Conclusion:
The force that must be applied to pump the small piston to lift the automobile is 6540 N.
- Mass of the automobile (m) = 2000 kg
- Area of the large piston (A1) = 30 cm² = 30 × 10⁻⁴ m² = 0.003 m² (conversion to m²)
- Area of the small piston (A2) = 10 cm² = 10 × 10⁻⁴ m² = 0.001 m² (conversion to m²)
- Weight (W) = mass × gravitational acceleration (g)
- Here, g = 9.81 m/s² (approximate value)
- W = 2000 kg × 9.81 m/s² = 19620 N
- According to Pascal's principle, the pressure applied on the small piston is equal to the pressure exerted by the large piston.
- Pressure (P) = Force (F) / Area (A)
- For the large piston:
P1=F1A1
- For the small piston:
P2=F2A2
- Since P1=P2, we can write:
F1A1=F2A2
- We know F1=W=19620N, A1=0.003m², and A2=0.001m².
- Substitute these values into the equation:
19620N0.003m²=F20.001m²
- Rearranging gives:
F2=19620N×0.001m²0.003m²
- Calculate F2:
F2=19620×0.0010.003=196203=6540N
- The force that must be applied to the small piston to lift the automobile is F2=6540N.
The force that must be applied to pump the small piston to lift the automobile is 6540 N.
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Conceptual Problems
Explore 103 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Advanced problems for competitions
Explore 21 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Long Answer questions
Explore 33 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
Similar Questions
To lift an automobile of 200kg. a hydraulic pump with a larger piston 900cm2 in area is employed. Calculate the force that must be applied to pump a small piston of area 10cm2 to accomplish this task.
View SolutionCalculate the length of the diagonal of a square if the area of the square is 32cm2.
View Solution
Knowledge Check
The perimeter of a square is 30 cm. Find its area (in cm2).
A56.25B112.5C60.25D120.5Two syringes of different cross-section (without needle filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston an larger piston are 1cm and 3cm respectively. If a force of 10N is applied to the smaller piston then the force exerted on the larger piston is
A30NB60NC90ND100N
Calculate the length of the diagonal of a square if the area of the square is 32cm2
View SolutionA car of mass 1400 kg placed on the platform in a service station has to be lifted up. The area of the press piston to which the platform is 5m2. Determine the force that has to be applied on the piston of pump cylinder having an area of cross section 0⋅25m2.
(Take g = 10 m s−2)
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
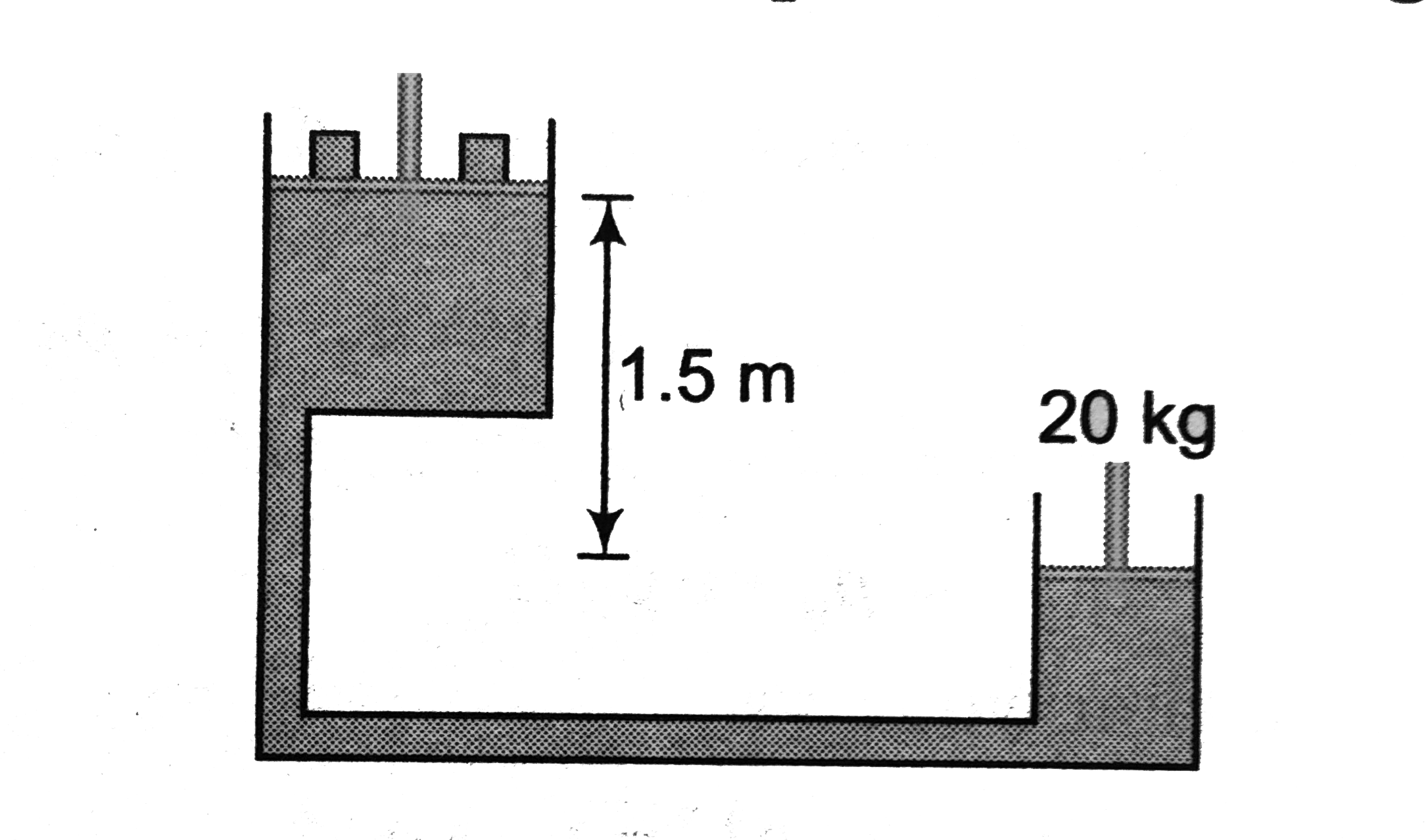 .
.
View SolutionIn a hydraulic lift, the area of smaller piston is 5cm2. The weight raised by larger piston is 900 kgf, if a force of 150 kg fis applied on smaller piston. Calculate the area of larger piston.
View SolutionThe area of smaller piston of a hydraulic pressure is 2cm square and that of larger piston is 20 cm square. How much weight can be raised on the larger piston when a force 200kg f is exerted on the smaller piston? g=10m/s2
View SolutionTwo pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger pistion when 40 kg wt. is placed on the smaller piston? If the smaller pistion moves in through 6 cm, how much does the other pistion move out ?
View Solution

