The rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
The rate of formation of SO3 in the following reaction,
2SO2+O2→2SO3 is 10gsec−1
The rate of disappearance of O2 will be:
(a) 5gsec−1
(b) 100gsec−1
(c ) 20gsec−1
(d) 2gsec−1
The correct Answer is:d
12d[SO3]dt=d[O2]dt
∴d[O2]dt=12×1080molsec−1
=12×1080×32=2gsec−1
Topper's Solved these Questions
- CHEMICAL KINETICSBook:P BAHADURChapter:CHEMICAL KINETICSExercise:Exercise 1
Explore 2 Videos
- CHEMICAL KINETICSBook:P BAHADURChapter:CHEMICAL KINETICSExercise:Exercise 3A
Explore 2 Videos
- DILUTE SOLUTION AND COLLIGATIVE PROPERTIESBook:P BAHADURChapter:DILUTE SOLUTION AND COLLIGATIVE PROPERTIESExercise:Exercise 9 Advanced Numerical
Explore 12 Videos
Similar Questions
The rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For the reaction, A+2B⇔AB2, the rate of forward reaction is dxdt=1×105[A][B]2−1×104[AB2]. The rate constants for forward and backward reactions are:
View SolutionThe rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For a gaseous reaction, the rate is expressed in terms of dPdt in place of dCdt or dndt where C is concentration, n is number of moles and 'P' is pressure of reactant. The three are related as:
View Solution
Knowledge Check
The rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For the reaction, aA→bB,
log[−dAdt]=log[dBdt]+0.6, then a:b is:A(a) 3.98B(b) 2.18C(c ) 1.48D(d) 0The rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For a hypothetical reaction aA+bB→ Product, the rate law is: rate =K[A]x[B]y, then:A(a) (a+b)=(x+y)B(b) (a+b)<(x+y)C(c ) (a+b)>(x+y)D(d) Any of theseThe rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
At the point of intersection of the two curve shown for the reaction: A→nB the concentration of B is given by:
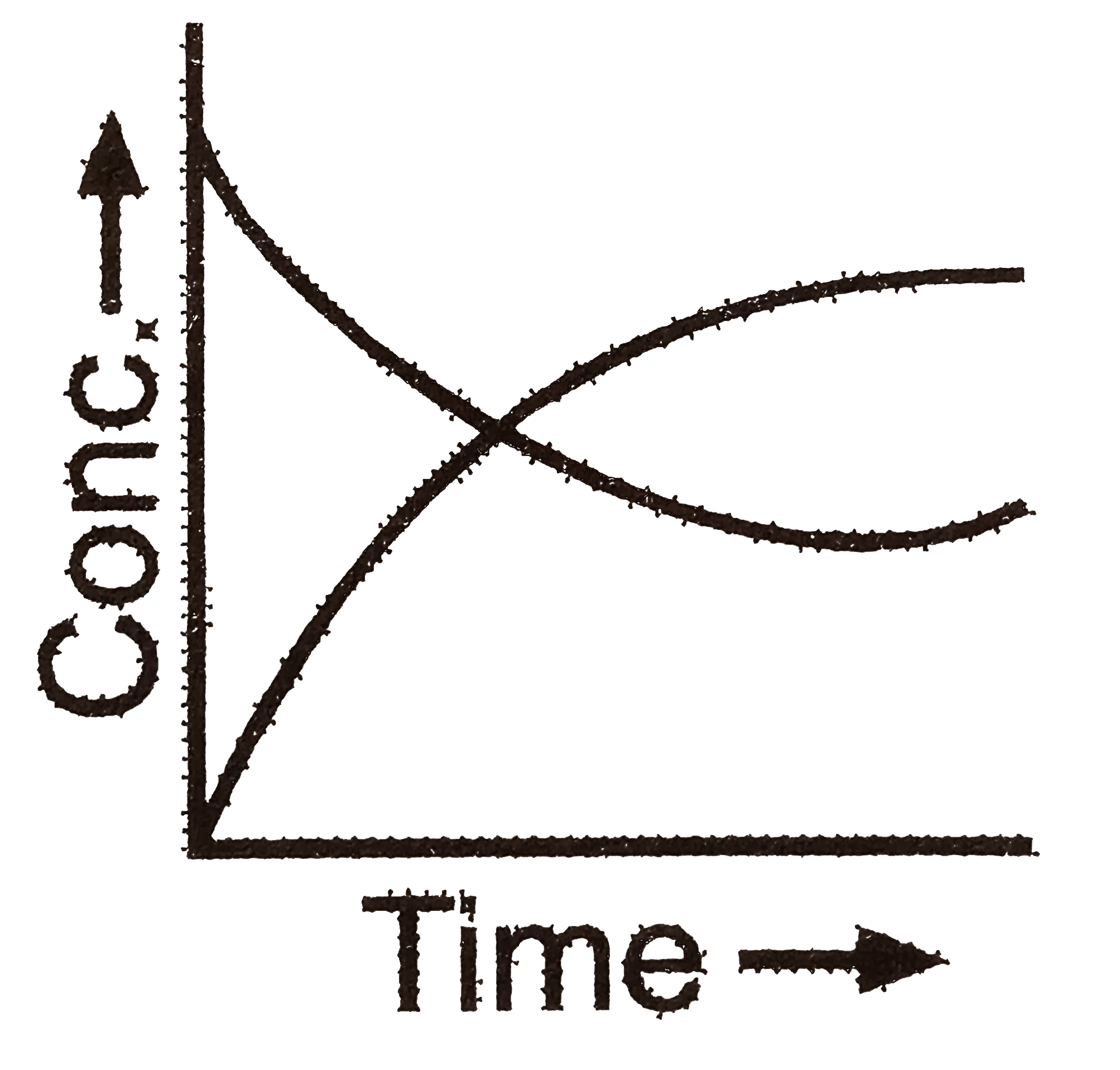 A(a) nA02B(b) A0n−1C(c ) nA0n+1D(d) (n−1)(n+1)A0
A(a) nA02B(b) A0n−1C(c ) nA0n+1D(d) (n−1)(n+1)A0
The rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For a reaction, 2ND3→N2+3D2,
−d[ND3]dt=K1[ND3],d[N2]dt=K2[ND3]
d[D2]dt=K3[ND3], then:
View SolutionThe rate and mechanism of chemical reactions are studied in chemical kinetics. The elementary reactions are single step reactions having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as :
rate = =(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or rate =K[A]a[B]b. In case of reversible reactions net rate expression can be written as : rate =K1[A]a[B]b–K2[C]c[D]d. At equilibrium, rate = 0. The constants K,K1,K2, are rate constants of respective reaction. In case of reactions governed by two or more steps reactions mechanism, the rate is given by the solwest step of mechanism.
The rate of formation of SO3 in the following reaction : 2SO2+O2→2SO3 is 10gsec−1. The rate of disapperance of O2 will be :
View SolutionThe rate and mechamical reaction are studied in chemical kinetics. The elementary reactions are single step reaction having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as:
rate=(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or expression can be written as : rate =K1[A]a[B]b−K2[C]c[D]d. At equilibrium, rate =0. The constants K,K1,K2 are rate constants of respective reaction. In case of reactions governed by two or more steps reaction mechanism, the rate is given by the slowest step of mechanism.
For the reaction, 2NO+Br2⇔2NOBr, the mechanism is given in two steps:
(1)NO+Br2fast⇐⇒NOBr2
(2)NOBr2+NOslow−−→2NOBr
The rate expression for the reaction is:
View SolutionThe rate and mechanism of chemical reactions are studied in chemical kinetics. The elementary reactions are single step reactions having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as :
rate = =(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or rate =K[A]a[B]b. In case of reversible reactions net rate expression can be written as : rate =K1[A]a[B]b–K2[C]c[D]d. At equilibrium, rate = 0. The constants K,K1,K2, are rate constants of respective reaction. In case of reactions governed by two or more steps reactions mechanism, the rate is given by the solwest step of mechanism.
For the reaction : aA→bB,
log[−dAdt]=log[dBdt]+0.6, then a:b is :
View SolutionThe rate and mechanism of chemical reactions are studied in chemical kinetics. The elementary reactions are single step reactions having no mechanism. The order of reaction and molecularity are same for elementary reactions. The rate of forward reaction aA+bB→cC+dD is given as :
rate = =(dxdt)=−1ad[A]dt=−1bd[B]dt=1cd[C]dt=1dd[D]dt or rate =K[A]a[B]b. In case of reversible reactions net rate expression can be written as : rate =K1[A]a[B]b–K2[C]c[D]d. At equilibrium, rate = 0. The constants K,K1,K2, are rate constants of respective reaction. In case of reactions governed by two or more steps reactions mechanism, the rate is given by the solwest step of mechanism.
For a reaction, 2ND3→N2+3D2:
−d[ND3]dt=K1[ND3],d[N2]dt=K2[ND3],d[D2]dt=K3[ND3], then :
View Solution

