The rate constant of decomposition of methyl nitrite and ethyl nitrite follow the equations.
and
Calculate the temperature at which both have same rate of decomposition if of each is taken and both show order kinetics.
Rate=
Since [Reactant]= and rates are same, thus at same temperature
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - P BAHADURCHAPTER - CHEMICAL KINETICSEXERCISE - Exercise 1
2 Videos
- CHEMICAL KINETICSBOOK - P BAHADURCHAPTER - CHEMICAL KINETICSEXERCISE - Exercise 3A
2 Videos
- DILUTE SOLUTION AND COLLIGATIVE PROPERTIESBOOK - P BAHADURCHAPTER - DILUTE SOLUTION AND COLLIGATIVE PROPERTIESEXERCISE - Exercise 9 Advanced Numerical
12 Videos
Similar Questions
The Arrehenius equation for the rate constant of decompoistion of methyl nitrite and ethyl nitrite are
k1(s−1)=1013exp(−152300Jmol−1RT)
and k2(s−1)=1014exp(−157700Jmol−1RT) respectively. Find the temperature at which the rate constant are equal.
View SolutionThe Arrhenius equations for cis-trans isomerzation of but-2-ene (CH3−CH=CH−CH3) and but-2-ene, 1 nitrile (CH3−CH=CH−CN) are,
k(s−1)=1013.8exp(−263.5kJmol−1/RT)
k−1(s−1)=1011exp(−214.5kJmol−1/RT) Calculate the temperature at which k=k−1.
View Solution
Knowledge Check
The rate constant for the first order decomposition of ethylene oxide into CH4 and CO,
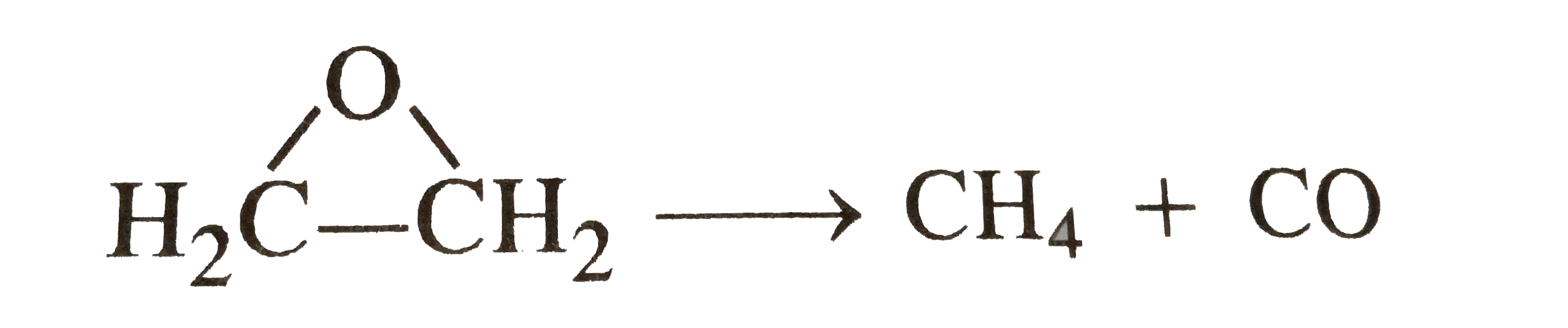
may be describe by
logk(ins−1)=14.34−1.25×104KT
The activation energy of the reaction isA4.8×10−5kJmol−1B4.8×105kJmol−1C2.39×102kJmol−1D2.39×105kJmol−1The rate constant of a reaction is given by k=2.1×1010exp(−2700/RT). It means that
Alog k versus 1T will be a straight line with slope =−27002.303RBlog k versus 1T will be a straight line with intercept on axis = 10.32CWhen T becomes infinite , k=2.1×1010Dk is independent of temperatureThe rate constant of a reaction is given by k=2.1×1010exp(−2700/RT). It means that
Alog k vs. 1/T will be a straight line with slope
=−27002.303 RBlog k vs. 1/T will be a straight line with intercept on log k axis =2.1×1010CThe number of effective collisions are 2.1×1010 cm−3 sec−1DHalf life of the reaction increases with increase of temperature.
The decomposition of hydrocarbon follows the equation k=(4.5×1011s−1)e−28000K/T
Calculate Ea.
View SolutionThe decomposition of hydrocarbon follows the equation k=(4.5×1011s−1)e−28000K/T
Calculate Ea.
View SolutionThe decomposition of hydrocarbon follows the equation k=(4.5×1011s−1)e−28000K/T. Calculate Ea.
View SolutionThe decomposition of hydrocarbon follows the equation k=(4.5×1011s−1)e−28000K/T
Calculate Ea.
View SolutionThe rate of decomposition for methyl nitrite and ethyl nitrite can be given in terms of rate constant (insec−1)K1 and K2 respectively. The energy of activation for the two reaction are 152.30kJmol−1 and 157.7kJmol−1 as well as frequency factor are 1013 and 1014 respectively for the decomposition of methyl and ethyl nitrite. Calculate the temperature at which rate constant will be same for the two reactions.
View Solution
