Show that zero is the identity for addition on R and 1 is the identity for multiplication on R. But there is no identity element for the operations −:R×R→Rand ÷:R⋅×R⋅→R⋅.
Video Solution
Text Solution
We know that
a+0=a=0+a
and a×1=a=1×a∀a∈R
⇒0 is the additive identity and 1 is the multiplicative identity in R.
a−e=a=e−a∀a∈R
∴ for− :R×R→R there is no identity element in R.
Similarly, for÷:R×R→R,there is no identity element in R.
Hence Proved.
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBook:NCERTChapter:RELATIONS AND FUNCTIONSExercise:EXERCISE 1.4
Explore 13 Videos
- RELATIONS AND FUNCTIONSBook:NCERTChapter:RELATIONS AND FUNCTIONSExercise:EXERCISE 1.2
Explore 12 Videos
- RELATIONS AND FUNCTIONSBook:NCERTChapter:RELATIONS AND FUNCTIONSExercise:EXERCISE 1.3
Explore 14 Videos
- PROBABILITYBook:NCERTChapter:PROBABILITYExercise:EXERCISE 13.2
Explore 18 Videos
- SETSBook:NCERTChapter:SETSExercise:EXERCISE 1.3
Explore 1 Video
Similar Questions
Knowledge Check
Identity P,Q,R and S in the diagram
 AP-negative regative, Q-inhibitor,R-effector molecule, S-positive regulationBP-positive regulation, Q-effector molecule, R-inhibitor,S-negative regulationCP-negative regulation, Q-inhibitor, R-positive regulation, S-effector moleculeDP-positive regulative, Q-effector molecule,R-negative regulation, Sinhibitor.
AP-negative regative, Q-inhibitor,R-effector molecule, S-positive regulationBP-positive regulation, Q-effector molecule, R-inhibitor,S-negative regulationCP-negative regulation, Q-inhibitor, R-positive regulation, S-effector moleculeDP-positive regulative, Q-effector molecule,R-negative regulation, Sinhibitor.Let '∗' be the binary operation defined on the set Z of all integers as a∗b=a+b+1 for all a, b ∈Z. The identity element w.r.t. this operations is
A−1B−2C1D0
If * defined on the set R of real numbers by a⋅b=3ab7 , find the identity element in R for the binary operation *.
View SolutionIf ∗ is a binary operation on the set R of all real numers difined by a∗b=a+b−3 then find the identity element for ∗.
View SolutionIdentity A, B, C, D, E, R and R' in the following:
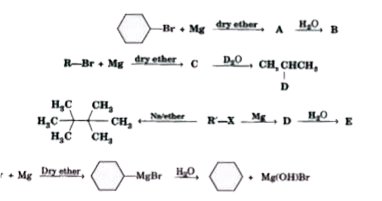
View SolutionIdentity A, B, C, D, E, R and R' in the following:

View SolutionThe whole number 0 (zero) is called the additive identity or the identity element for addition of whole numbers.
View SolutionShow that addition and multiplication are associative binary operation on R. But subtraction is not associative on R. Division is not associative on R*.
View Solution